Главная » CADmaster №5(78) 2014 » Машиностроение Моделирование конкурентного роста зерен при направленной кристаллизации никелевого жаропрочного сплава
Введение
При использовании беззатравочной технологии, на начальном этапе получения монокристаллической отливки происходит конкурентный рост множества зародившихся зерен, приводящий к отбору одного зерна с преимущественной кристаллографической ориентировкой.
Известно, что для роста дендрита, образующего зерно, необходимо переохлаждение расплава, определяемое как разность температуры равновесного ликвидуса данного сплава и температуры вблизи вершины первичной оси дендрита. Известно также, что преимуществом в конкурентном росте обладают зерна с кристаллографической ориентацией [001], имеющей наименьшее отклонение от вектора градиента температуры. Согласно модели, предложенной Уолтоном и Чалмерсом [1], для роста зерна с преимущественной кристаллографической ориентацией требуется наименьшее переохлаждение расплава. Поэтому такое зерно опережает зерна с другой кристаллографической ориентацией и постепенно вытесняет их.
Модель [1] нашла экспериментальное подтверждение на бикристаллических отливках никелевых жаропрочных сплавов в случае роста двух расходящихся зерен, одно из которых имеет ориентацию [001] [ 2, 3, 4, 5 ]. Работа [3] подтверждает основополагающий тезис модели Уолтона и Чалмерса об опережении зерном с ориентацией [001] прочих зерен. Экспериментально показано, что зерна с кристаллографическим направлением [001] опережают как расходящиеся, так и сходящиеся зерна. Вместе с тем, известны экспериментальные данные, свидетельствующие об отсутствии подавления зерном с ориентацией [001] сходящегося с ним зерна [4, 5] либо о вытеснении зерна с ориентацией [001] сходящимся с ним зерном [2, 3], что противоречит модели Уолтона и Чалмерса. В работе [6] сделано предположение, что результаты, противоречащие геометрической модели Уолтона и Чалмерса, можно объяснить взаимодействием диффузионных полей конкурирующих дендритов, которое приводит к подавлению роста вторичных ветвей.
Согласно модели [1], величина отставания вершины дендрита должна зависеть от условий кристаллизации, то есть локальных значений градиента температуры G и скорости кристаллизации W. В экспериментальных исследованиях обычно оперируют технологическими параметрами процесса — скоростью перемещения формы и оценочной величиной градиента температуры для данной установки, которые могут значительно отличаться от истинных условий кристаллизации данного сечения отливки [7]. Поскольку способы оценки градиента температуры у разных авторов могут различаться, это затрудняет сравнение экспериментальных данных.
В связи со сложностью определения локальных условий кристаллизации в натурном эксперименте, для исследования конкурентного роста может быть проведен вычислительный эксперимент с использованием модуля CAFE системы ProCAST [8]. В работах [ 9, 10, 11 ] экспериментально подтверждена адекватность программного модуля и модели CAFE и проведены исследования конкурентного роста зерен в спиральных кристаллоотборниках различных размеров при направленной кристаллизации никелевых жаропрочных сплавов.
В настоящей работе с помощью численного моделирования в модуле CAFE системы ProCAST проведено систематическое исследование влияния условий кристаллизации на конкурентный рост зерен в отливке из сплава ЖС26 в виде пластины в широком диапазоне значений градиента температуры и скорости кристаллизации.
Методика вычислительного эксперимента
Для моделирования роста зерен был использован модуль CAFE системы компьютерного моделирования литейных процессов ProCAST. Моделировался процесс направленной кристаллизации тонкой пластины с размерами 200×40×4 мм при заданных градиенте температуры G в двухфазной зоне и скорости перемещения изотермы ликвидус W, которые оставались постоянными на протяжении всего процесса кристаллизации. Предполагалось, что на нижнем торце пластины зародились три зерна (А, B и A, рис. 1) заданной кристаллографической ориентации. Возможность образования каких-либо еще зерен, например, перед фронтом роста или на границах пластины (паразитные зерна) не рассматривалась.
Азимутальная ориентация всех зерен была таковой, что боковые грани пластины были параллельны кристаллографической плоскости (001). Во всех расчетах зерна типа A были ориентированы таким образом, что одно из кристаллографических направлений [001] совпадало с продольной осью пластины. Отклонение кристаллографического направления [001] от оси отливки зерна B варьировалось в пределах α=5÷54°. В модуле CAFE ориентация зерен задается углами Эйлера (φ1, φ, φ2), где угол φ1 определяет азимутальный разворот кристаллографической решетки, а угол φ определяет отклонение первичных осей дендритов от вектора градиента температуры. Таким образом, кристаллографическая ориентация зерен А всегда была задана углами φ1=0, φ=0, φ2=0. Кристаллографическая ориентация зерна В менялась следующим образом: φ1=0, φ=α, φ2=0.
Азимутальная ориентация всех зерен была таковой, что боковые грани пластины были параллельны кристаллографической плоскости (001). Во всех расчетах зерна типа A были ориентированы таким образом, что одно из кристаллографических направлений [001] совпадало с продольной осью пластины. Отклонение кристаллографического направления [001] от оси отливки зерна B варьировалось в пределах. В модуле CAFE ориентация зерен задается углами Эйлера (φ1, φ, φ2), где угол φ1 определяет азимутальный разворот кристаллографической решетки, а угол φ определяет отклонение первичных осей дендритов от вектора градиента температуры. Таким образом, кристаллографическая ориентация зерен А всегда была задана углами φ1=0, φ=0, φ2=0. Кристаллографическая ориентация зерна В менялась следующим образом: φ1=0, φ=α, φ2=0.
Условия роста зерен при направленной кристаллизации, то есть параметры и, меняются по длине отливки, даже если это отливка простой геометрической формы и постоянного сечения [12]. Поэтому структура в данном сечении отливки зависит не только от текущих условий кристаллизации, но и от предыстории роста зерен. Чтобы избежать этого влияния и обеспечить однозначное соответствие результатов конкурентного роста текущим условиям кристаллизации, в расчете были использованы модельные распределения температуры, отвечающие следующим требованиям: радиальный градиент температуры равен нулю, постоянный осевой градиент по всей двухфазной зоне и постоянная скорость перемещения изотермы ликвидус. Этим условиям удовлетворяет линейное распределение температуры в двухфазной зоне T=G(x-xs)+Ts, G=const, xs=Wτ. Распределения температуры были рассчитаны в тепловом модуле системы ProCAST с применением модуля UserFunction и использованы в качестве исходных данных для моделирования роста зерен в модуле CAFE.
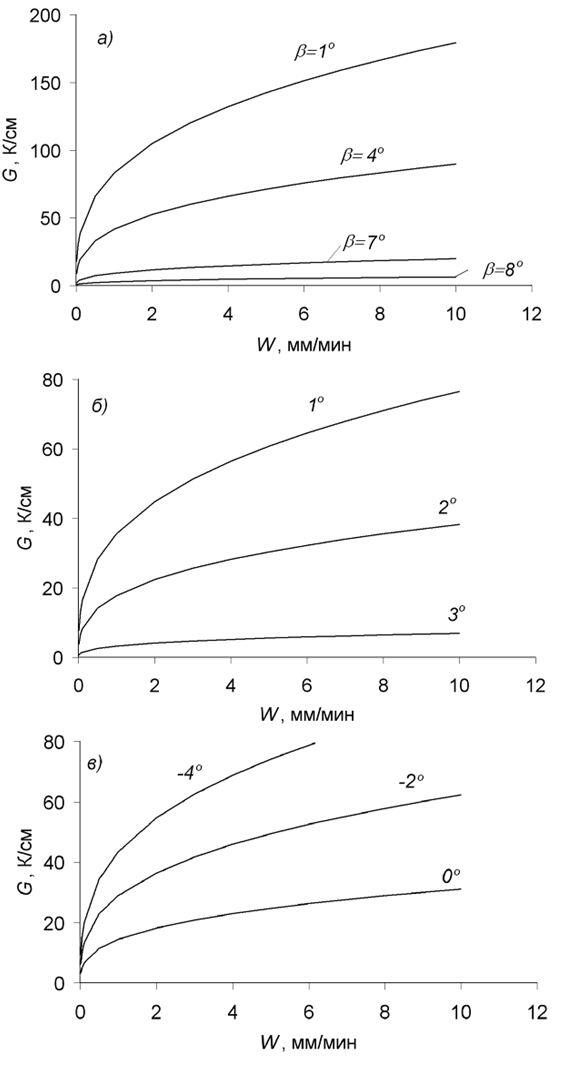
Расчеты проводились для значений градиента температуры 5, 10, 40, 70, 100 и 300 К/см и скорости кристаллизации 1, 5 и 10 мм/мин, что практически охватывает весь диапазон градиентов температуры и скоростей кристаллизации, наблюдаемых при кристаллизации отливки типа рабочей лопатки газотурбинной установки.
Коэффициенты кинетического уравнения, связывающего скорость роста вершины дендрита V с переохлаждением ▲T — V=a2▲T2+a3▲T3 были рассчитаны с помощью модуля CAFE. Необходимые для этого данные — наклон поверхности ликвидуса mi и коэффициент распределения ki — были оценены по бинарным диаграммам состояния систем на основе Ni с основными легирующими элементами сплава ЖС26. Химический состав сплава ЖС26 и данные для расчета коэффициентов и приведены в таблице 1. Коэффициент Гиббса-Томсона Г, характеризующий влияние кривизны поверхности раздела фаз на переохлаждение расплава, и коэффициент диффузии в расплаве, также необходимые для расчета a2 и a3, приведены в таблице 2.
| Элемент | С | Сг | Со | Мо | W | Nb | А1 | Ti | V | Ni |
|---|---|---|---|---|---|---|---|---|---|---|
| Концентрация | 0.15 | 4.9 | 9.0 | 1.1 | 11.7 | 1.7 | 5.9 | 1.0 | 0.9 | Осн. |
| мае. % | ||||||||||
| т, 1 К | - | -1.4 | - | -4 | 11.9 | -2.3 | -3.5 | -11 | -5.5 | - |
| к | - | 0.9 | - | 0.8 | 0.67 | 0.34 | 0.85 | 0.88 | 0.7 | - |
| Коэффициент Гиббса-Томсона, Г | Км | 2·10-7 |
| Коэффициент диффузии в расплаве, DL, [15] | м2сек-1 | 1·10-9 |
| α2 | мсек-1К-2 | 0 |
| α3 | мсек-1К-3 | 3.44.10-6 |
Согласно теории Уолтона и Чалмерса [1] зерно с преимущественной кристаллографической ориентацией подавляет соседей, поскольку их опережает. Предложенная в [13] схема конкурентного роста зерен в несколько измененном виде представлена на рис. 2. В установившемся режиме кристаллизации аксиальная составляющая скорости роста дендрита равна скорости изотермы ликвидуса, то есть V cosa=W, где — угол отклонения направления [001] от вектора градиента температуры. Отставание вершины дендрита от поверхности равновесного ликвидуса определяется выражением h=▲T/G, где ▲T — переохлаждение перед вершиной дендрита. Воспользовавшись выражением (1), можно получить выражение для величины отставания ▲h=hB-hA зерна В от зерна A (см. рис. 1) в следующем виде:
▲h=(W/a3)1/3(cos-1/3α-1)/G) (2)
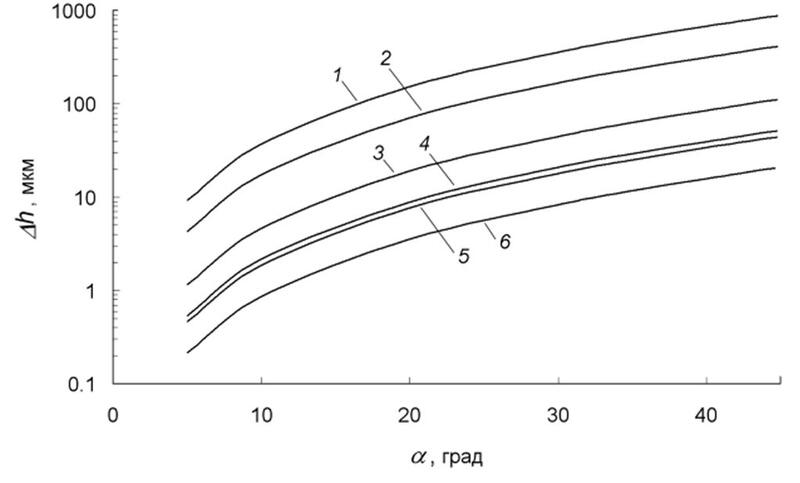
Как следует из (2), величина «ступеньки» на фронте роста между зернами A и B зависит от градиента температуры и, в меньшей степени, от скорости продвижения фронта. Кривые изменения в зависимости от ориентации зерен и параметров процесса кристаллизации показаны на рис. 3.
В модуле CAFE с использованием метода клеточных автоматов имитируется рост твердой фазы на регулярной объемной сетке с кубической ячейкой [14]. Перемещение фронта твердой фазы происходит по направлениям [001] рассматриваемых зерен. Движение по направлению [001] можно представить как сумму перемещений в направлении нормалей к граням ячеек сетки. Если верно, что в конкурентном росте важную роль играет отставание зерна В, то можно предположить, что сетка должна быть достаточно мелкой, чтобы адекватно описать «ступеньку» на фронте роста зерен с различной кристаллографической ориентацией, то есть размер ячейки должен быть меньше ▲h. В этом случае твердая фаза получает возможность бокового роста, приводящего к подавлению отстающего зерна.
Типичная макроструктура отливки, полученная в вычислительном эксперименте, представлена на рис. 1. Граница между зернами A и B является плоскостью, а линия ее пересечения с боковыми границами отливки — прямой линией, что объясняется постоянством градиента температуры и скорости перемещения изотермы ликвидуса. В результате совместного роста зерен, как правило, происходит смещение границы между зернами в сторону зерна В, то есть происходит вытеснение зерна В, имеющего ненулевой угол отклонения направления роста [001] от вектора градиента температуры. Интенсивность вытеснения зерна В характеризуется углом наклона границы зерен .
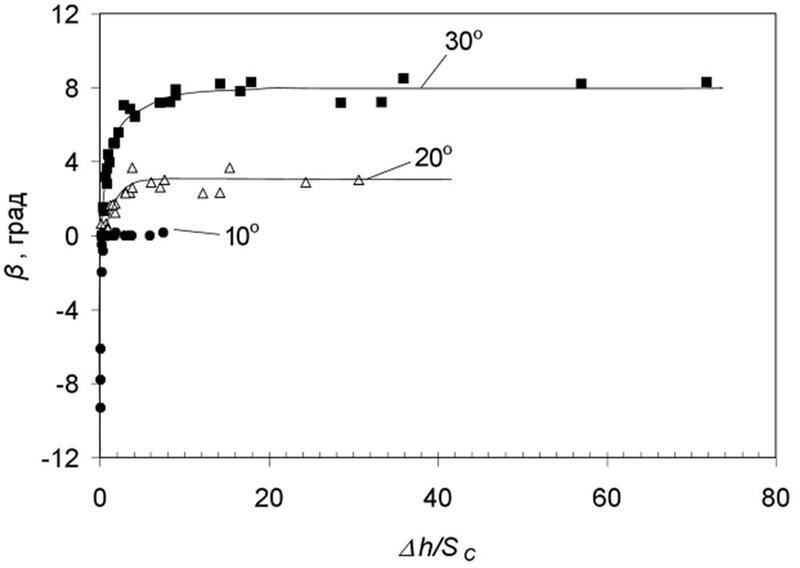
Расчеты, проведенные для различных градиентов температуры и скоростей кристаллизации в диапазонах G=5, 10, 40, 100 К/см и W=1, 5, 10 мм/мин. показали, что угол отклонения границы сходящихся зерен при фиксированном угле α однозначно определяется единственным параметром — отношением ▲h/Sc (рис. 4).
Расчеты проводились при SC=5 и 20 мкм. Для G=40 К/см и W=1, 10 мм/мин. дополнительно были проведены расчеты при SC=40, 50 и 80 мкм.
При ▲h/Sc больше некоторой величины ▲ha, зависящей от угла α, результат моделирования не зависит ни от выбора Sc, ни от условий кристаллизации. Как видно из рис. 4, при α=30°▲hα≈20, то есть размер ячейки многократно меньше «ступеньки» на фронте роста.
При ▲h/Sc<▲hα результат моделирования полностью зависит от этого параметра. Даже, несмотря на значительное отклонение зерна В от преимущественной ориентации (α=30°), при значениях ▲h/Sc<▲hα угол отклонения границы β резко уменьшается с уменьшением параметра ▲h/Sc.
Уменьшение ▲h/Sc может быть связано с условиями кристаллизации — с высоким градиентом температуры G и/или низкой скоростью кристаллизации W, при которых ▲h->0, либо с выбором грубой сетки, то есть когда Sc≥▲h. Таким образом, для получения результатов моделирования, адекватных реальной картине конкурентного роста, правильный выбор Sc имеет решающее значение.
Величину Sc следует выбирать, опираясь на аналогию между распространением твердой фазы по ячейкам кубической сетки и ростом ветвей дендритов, то есть исходя из параметров дендритной структуры, которая формируется при данных условиях кристаллизации.
В случае сходящихся зерен одним из возможных механизмов подавления отстающего зерна является механическое препятствование его росту. В работе [16] было сделано предположение, что эффективное подавление отстающего зерна возможно в том случае, если лидирующее зерно опережает своих конкурентов на величину, равную и большую расстоянию между вторичными осями дендритов λ2. Это позволяет свободно развиваться вторичным ветвям лидирующего зерна перед вершинами дендритов отстающего зерна и тем препятствовать его росту. В работе [13], ссылаясь на экспериментальные результаты, полученные на прозрачных органических веществах, полагали, что к боковому росту способны лишь некоторые вторичные ветви дендрита, расстояние между которыми составляет несколько λ2, и размер сетки следует соотносить с этим расстоянием.
В работах [3, 6] были измерены расстояния между вторичными осями дендритов на отливках, закаленных из процесса направленной кристаллизации. Было установлено, что на начальной стадии развития вторичных осей равно 10−15 мкм. Ориентируясь на результаты этих исследований, было принято, что размер элементарной ячейки расчетной сетки должен выбираться в диапазоне 5−20 мкм.
Результаты вычислительного эксперимента
Расходящиеся зерна, Sc=5 мкм. В случае с расходящимися зернами (рис. 5а и 5б), отставание зерна В не играет существенной роли, поскольку вытеснение зерна В происходит путем распространения вторичных ветвей дендрита зерна A в боковой зазор между зернами [3, 5].
Вытеснение зерна В наблюдается во всем исследованном диапазоне углов α от 5° до 45°. Изменение угла β в этом диапазоне очень хорошо описывается зависимостью β=0.5α, что вполне согласуется с результатами работы [5].
Уменьшение угла β при углах α<45° связано с изменением статуса зерна В. Из расходящегося зерна оно превращается в сходящееся, поскольку наименьший угол отклонения от вектора градиента температуры будет иметь направление [001], направленное не от зерна, а к зерну А. Поэтому значения угла при для расходящихся зерен приблизительно равны значениям при для сходящихся зерен.
Сходящиеся зерна, Sc=5 мкм. Результаты, представленные на рис. 5в и 5 г, показывают, что в случае сходящихся зерен при углах α<20° вытеснение зерна B практически не происходит. Этот результат также согласуется с экспериментальными данными, приведенными в [2, 5, 6, 10]. Согласно теории, в случае со сходящимися зернами зерно B блокируется вторичными ветвями дендрита зерна A. Для реализации этого механизма конкурентного роста необходимо, чтобы зерно A опережало зерно B на расстояние, превышающее Sc. При α<20° величина опережения ▲h близка по величине к размеру элементарной ячейки Sc (рис. 3), что затрудняет боковое распространение фронта твердой фазы.
При больших углах α отставание зерна B от зерна A существенно больше размера элементарной ячейки, что позволяет зерну А свободно распространяться перпендикулярно градиенту температуры и блокировать соседа. Как и для расходящихся зерен, при α>20° угол наклона границы β сходящихся зерен может быть аппроксимирован линейной зависимостью β=0.5(α-20°).
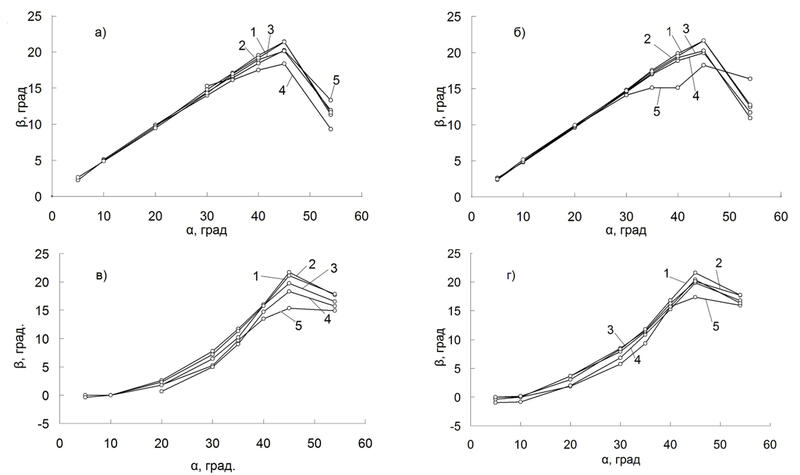
Влияние размера сетки. Результаты, представленные на рис. 6, получены при моделировании конкурентного роста на расчетной сетке с размером ячейки SC=20 мкм.
|
G, К/см |
W, мм мин. |
αA град |
αB град |
α = αA-αB град |
β, Град. | Источник |
|---|---|---|---|---|---|---|
| 90 | 10 | 0 | 15÷25 | 15÷25 | β = 0.5α | [5] |
| 20 | 3.5 | 0 | 15÷25 | 15÷25 | β = 0.5α | [5] |
| 128 | 1 | 0 | 10÷30 | 10÷30 | β = 0.25(α-8) + 3.5 | [3] |
| 30 | 3÷4.7 | 7 | 20 | 13 | 0 | [б] |
| 70 | 1.5÷2.5 | 7 | 20 | 13 | 0 | [б] |
В случае расходящихся зерен (рис. 6а и рис. 6б), при градиенте температуры более 100 К/см и углах α<10° происходит совместный рост зерен A и B без вытеснения последнего, что связано, по-видимому, с тем, что в этих условиях зазор между зернами существенно меньше и, потому неразличим при данном размере сетки. Эти результаты могут быть подкреплены экспериментальными данными [6], приведенными в таблице 3.
При малом градиенте температуры, то есть в условиях, когда зазор между зернами A и B соизмерим или больше Sc, результаты, представленные на рис. 6а и 6б (кривые 1−3), в целом схожи с результатами, представленными на рис. 5а и рис. 5б.
В случае сходящихся зерен при градиенте температуры более 40 К/см и углах α<20° зерно B вытесняет зерно A. В целом это подтверждается экспериментальными исследованиями [3]. Однако в данный момент объяснение этого результата в рамках геометрической модели взаимодействия зерен отсутствует.
Сравнение рис. 5 и рис. 6 показывает, что выбор размера сетки способен существенно изменить результаты моделирования. На мелкой сетке результаты моделирования для расходящихся зерен показывают безусловное подавление зерном А зерен с другими кристаллографическими ориентировками. Происходит также подавление сходящихся зерен при условиях кристаллизации, для которых ▲h существенно больше Sc.
Увеличение Sc приводит к результатам, предсказывающим трудности с подавлением сходящихся и расходящихся зерен В с углом отклонения α<20° при низкой скорости кристаллизации и высоком градиенте температуры. По существу Sc является настроечным параметром модели CAFE, который должен быть согласован с физической картиной конкурентного роста исходя из аналогии между распространением твердой фазы по ячейкам равномерной сетки и боковым ростом вторичных осей дендритов.
Сравнение с экспериментом
В таблицах 3 и 4 представлены экспериментальные данные для бикристаллических отливок из никелевых жаропрочных сплавов. Трудность их сравнения с результатами моделирования состоит в том, что для идентификации режимов, в которых были получены отливки, в одних работах указаны градиент температуры и скорость перемещения формы, в других — градиент температуры и расстояние между первичными осями дендритов или скорость перемещения формы и λ1. В целях сравнения с результатами, представленными на рис. 6 и рис. 7, недостающие значения G и W были рассчитаны с помощью зависимости λ1=620(GW)-0,333 [17, 5]. Предполагалось, что указанные в литературе значения скорости перемещения формы могут быть приняты за скорость кристаллизации W. Подготовленные таким образом данные были наложены на результаты моделирования. Как видно из рис. 6, имеется качественное совпадение вычислительного и натурного эксперимента.
Для расходящихся зерен в работе [5] предложены выражения для расчета угла наклона границы β в зависимости от угла α. Рассчитанные по ним углы хорошо согласуются с вычислительным экспериментом. Результаты по расходящимся зернам, полученные в работе [3], относятся к направленной кристаллизации с градиентом температуры 128 К/см. Учитывая возможную ошибку определения градиента при помощи термопар, можно говорить о том, что эти данные удовлетворительно согласуются с результатами вычислительного эксперимента при G=100 K/см и W=1 мм/мин. на сетке SC=20 мкм (рис. 6а).
Экспериментальные данные по сходящимся зернам свидетельствуют об отсутствии вытеснения зерен В [2, 5, 6] или о подавлении зерна A зерном В [3]. Вычислительный эксперимент качественно совпадает с этими результатами. На сетке с размером ячейки 5 мкм β<1°÷2° при углах α<20°, что согласуется с данными [2, 5, 6], а на сетке с размером ячейки 20 мкм зерно B вытесняет зерно A в диапазоне ориентировок при градиенте температуры больше 100 К/см, что согласуется с данными [3]. Эти результаты еще раз демонстрируют зависимость результатов моделирования от настроечного параметра Sc. С другой стороны, результаты [2, 5, 6] относятся к режимам кристаллизации, при которых опережение зерном А зерна В, рассчитанное по (2), лежит в узком интервале ▲h/λ2 (табл. 4). Таким образом, отливки, на которых проводились исследования, получены в условиях, близких с точки зрения конкурентного роста, что объясняет схожесть результатов, полученных в [2, 5, 6]. Согласно рис. 5, в этих условиях роста угол наклона границы мал, то есть не происходит вытеснение зерна В, что и подтверждается экспериментальными данными.
|
G К/см |
W мм/мин. |
αА, град |
αB, град |
αA-αB, град |
β, град |
▲h, мкм | ▲h/λ2 1 | Источник |
|---|---|---|---|---|---|---|---|---|
| 30 | 1,62 | 0 | 7 | 7 | 0 | 5,0 | 0,2 | [2] |
| 70 | 1,62 | 0 | 7 | 7 | 0 | 2,0 | 0,1 | [2] |
| 90 | 10 | 0 | 25 | 25 | 0 | 42 | 2 Л | [5] |
| 20 | 3.5 | 0 | 25 | 25 | 0 | 132 | 6.6 | [5] |
| 90 | 10 | 0 | 15 | 15 | 0 | 14 | 0,71 | [5] |
| 128 | 1 | 0 | 10 | 10 | -3.2 | 2.0 | 0.1 | [3] |
| 128 | 1 | 0 | 18 | 18 | -4 | 6.8 | 0.34 | [3] |
| 128 | 1 | 0 | 23 | 23 | -3.8 | 11.4 | 0,57 | [3] |
| 128 | 1 | 0 | 30 | 30 | -3.2 | 20.5 | 10 | [3] |
| 30 | 3÷4.7 | 7 | 20 | 13 | 0 | 20 | 1.0 | [б] |
| 70 | 1.5÷2.5 | 7 | 20 | 13 | 0 | 8 | 0.4 | [б] |
Практические рекомендации
Градиент температуры и скорость кристаллизации являются технологическими параметрами, которые важно контролировать в процессе кристаллизации.
Выше были представлены результаты, указывающие на то, что угол наклона границы конкурирующих зерен β однозначно определяется отношением величин ▲h и дисперсности дендритной структуры. В реальном β=f(▲h/Sc) процессе дисперсность структуры характеризуется расстоянием между вторичными осями дендритов, а в модели CAFE — параметром. С помощью выражения (2) зависимость, построенная по результатам вычислительных экспериментов, может быть преобразована к виду, позволяющему выработать практические рекомендации по выбору параметров технологического процесса.
На рис. 7 линиями постоянного угла β ограничены области режимов роста в координатах G-W. Подавление зерен с ориентацией α≥20° (рис. 7а и рис. 7б) происходит в диапазоне градиентов температуры, ширина которого зависит от скорости роста и угла α. С уменьшением градиента температуры увеличивается угол наклона границы β, то есть увеличивается скорость вытеснения зерна В. С уменьшением разориентации зерен (с уменьшением угла α) уменьшается максимальный градиент температуры, при котором возможно подавление зерна В. При углах разориентации α≤10° (рис. 7в), при низких градиентах температуры происходит совместный рост зерен (β=0), а при высоких градиентах — напротив, зерно В подавляет зерно А. Подавление зерна А экспериментально наблюдалось в работе [3] (см. табл. 4), при углах α≥10° .
В случае сходящихся зерен при любых градиентах температуры и скоростях кристаллизации происходит вытеснение зерен В.
Таким образом, для эффективного отбора зерен с преимущественной ориентацией (типа А) благоприятны режимы с невысоким градиентом температуры и большой скоростью роста. Однако подавление зерен с разориентацией менее 10 градусов проблематично: результатом конкурентного роста является либо бикристалл, либо монокристалл с ориентацией зерна В, то есть с отклонением от направления [001]. Если для подавления сильно разорентированных зерен предпочтителен низкий градиент температуры, то для получения такого монокристалла нужно увеличивать градиент температуры.
Выводы
- Результат моделирования конкурентного роста сходящихся зерен с аксиальной разориентацией может быть поставлен в зависимость от единственного параметра — отношения ▲h/Sc. Пределы чувствительности результата к этому параметру зависят от угла разориентации зерен α.
- Опираясь на аналогию распространения твердой фазы по равномерной сетке в методе клеточных автоматов с ростом дендрита по направлениям [001], можно предположить, что результат конкурентного роста зависит не только от опережающего роста зерна с преимущественной ориентацией, то есть величины ▲h, но и от расстояния между вторичными осями дендритов λ2.
- Результаты моделирования в модуле CAFE системы ProCAST хорошо согласуются с известными экспериментальными данными, что позволяет использовать эту модель для изучения роста зерен в условиях, вызывающих затруднения с точки зрения постановки эксперимента.
- С помощью вычислительного эксперимента получены закономерности изменения угла β наклона границы между зернами в зависимости от угла их разориентации α, градиента температуры на изотерме ликвидус G и скорости ее перемещения W, в диапазоне значений, характерном для технологического процесса получения монокристаллической отливки из никелевого жаропрочного сплава.
- Для отбора зерен с преимущественной ориентацией благоприятны режимы с невысоким градиентом температуры и большой скоростью роста. Эффективность отбора падает с уменьшением угла разориентации зерен.
Литература
- Walton D., Chalmers B. The origin of the preferred orientation in the columnar zone of ingots // Transaction of AIME 1959. V.215. P. 447−452.
- D’Souza N., Ardakani M.G., Wagner A., Shollock B.A., McLean M. Morphological aspects of competitive grain growth during directional solidification of a nickel-base superalloy, CMSX4 // Journal of Materials Science 2002. V.37. P.481−487.
- D’Souza N., Ardakani M.G., Wagner A., Shollock B.A., McLean M. Morphological aspects of competitive grain growth during directional solidification of a nickel-base superalloy, CMSX4 // Journal of Materials Science 2002. V.37. P.481−487.
- Zhao Xinbao, Liu Lin, Zhang Weiguo, Qu Min, Zhang Jun, Fu Hengzhi. Analysis of Competitive Growth Mechanism of Stray Grains of Single Crystal Superalloys during Directional Solidification Process // Rare Metal Materials and Engineering 2011. V.40.
№ 1 . P. 9−13. - Толорайя В.Н.,
Каблов Е.Н. , СветловИ.Л. Ростовая структура при направленной кристаллизации никелевых жаропрочных сплавов // Металловедение и термическая обработка. 2006.№ 8 . C. 25−32. - Wagner A., Shollock B.A., McLean M. Grain structure development in directional solidification of nickel-base superalloys // Materials Science and Engneering A. 2004. V.374. P. 270−279.
- Монастырский
В.П. Моделирование и оптимизация процесса направленной кристаллизации рабочих лопаток ГТД // Литейщик России. 2009.№ 7 . C. 18−23. - ProCAST, торговая марка ESI Group, France, www.esi-group.com.
- Carter P., Cox D.C., Gandin C.A., Reed R.C. Process modeling of grain selection during the solidification of single crystal superalloy castings // Materials Science and Engineering. 2000. V. A280. P. 233−246.
- Dai H.J., Dong H.B., D’Souza N., Gebelin J.-C., Reed R.C. Grain Selection in Spiral Selectors During Investment Casting of Single-Crystal Components: Part II. Numerical Modeling // Metallurgical and Materials Transactions A. 2011. V. 42A. Nov. P. 3439−3446.
- Chubin Yang, Lin Liu, Xinbao Zhao, Ning Wang, Jun Zhang, Hengzhi Fu. Competitive grain growth mechanism in three dimensions during directional solidification of a nickel-based superalloy // Journal of Alloys and Compounds. 2013. V. 578. P. 577−584.
- Монастырский В.П., Кондратьева
М.С. Моделирование направленной кристаллизации отливок из никелевых жаропрочных сплавов в установке с водоохлаждаемым кристаллизатором // Литейщик России. 2013.№ 1 . C. 23−27. - Rappaz M., Gandin Ch.-A. Probabilistic Modelling of Microstructure Formation in Solidification Processes // Acta Metall.Mater. 1993. V.41.
№ 2 . P. 345−360. - Rappaz M., Gandin Ch.-A. Probabilistic Modelling of Microstructure Formation in Solidification Processes // Acta Metall.Mater. 1993. V.41.
№ 2 . P. 345−360. - Xiaoli Yang, Dylan Ness, Lee P.D., D’Souza N. Simulation of stray grain formation during single crystal seed melt-back and initial withdrawal in the Ni-base superalloy CMSX4 // Materials Science and Engineering A 2005. V.413−414. P. 571−577.
- Монастырский В.П.,
Качанов Е.Б. , НаумовМ.И. Математическая модель конкурентного роста столбчатых зерен при направленной кристаллизации многокомпонентного расплава // Труды IV Всесоюзной конференции по проблемам кристаллизации сплавов и компьютерного моделирования «Кристаллизация и компьютерные модели», Ижевск: УдГУ. 1991. C. 10−24. - Светлов И.Л.,
Кулешова Е.А. ,Монастырский В.П. ,Толорайя В.Н. ,Кривко А.И. ,Панкратов В.А. ,Орехов Н.Г. ,Башашкина Е.В. , ГоловкоБ.А. Влияние направленной кристаллизации на фазовый состав и дисперсность структуры никелевых сплавов //Известия АН СССР. Металлы. 1990.№ 1 . C. 86−93.
- При расчете было принято, что λ2=20 мкм ↑
Валерий Монастырский,
Михаил Ершов
МГМУ «МАМИ»
Алексей Монастырский
CSoft
Тел.: (495) 069−4488
E-mail: avmon@csoft.ru
Скачать статью в формате PDF — 2.17 Мбайт |

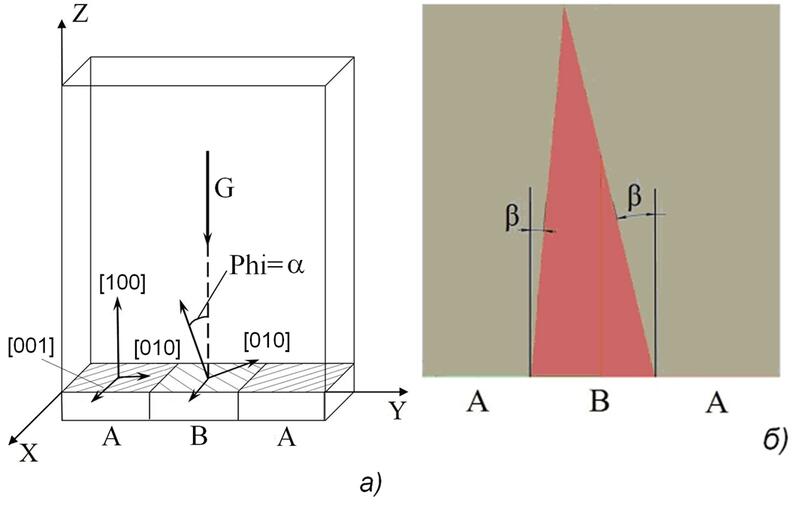
![Рис. 2. Схема роста зерен с различной кристаллографической ориентацией по [13]](https://www.cadmaster.ru/800x/assets/images/articles/cm_78_10/img02.jpg)
![Рис. 6. Угол границы между зернами в зависимости от ориентации зерна В. а - расходящиеся зерна, W=1 мм/мин.; б - расходящиеся зерна, W=10 мм/мин.; в - сходящиеся зерна, W=1 мм/мин.; г - сходящиеся зерна, W=10 мм/мин.; Расчет: 1 - G=5 K/см; 2 - G=10 K/см; 3 - G=40 K/см; 4 - G=100 K/см; 5 - G=300 K/см. Эксперимент: 6 - [3]; 7 - [5]; 8 - [6]; 9 - [2]](https://www.cadmaster.ru/800x/assets/images/articles/cm_78_10/img06.jpg)