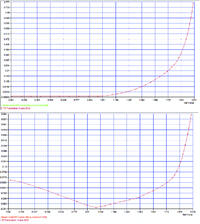
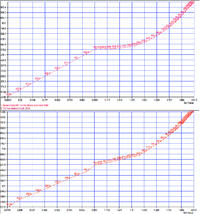
Главная » CADmaster №2(57) 2011 » Архитектура и строительство Применение оболочечных и объемных элементов при расчетах строительных стальных конструкций в программах SCAD и Nastran c учетом геометрической и физической нелинейности
1. Область возможного применения расчетных моделей с использованием оболочечных и объемных конечных элементов при проектировании стальных конструкций
Расчетные модели с использованием оболочечных конечных элементов имеют ряд преимуществ по сравнению со стержневыми моделями, а в некоторых случаях их применение может дать существенный эффект с точки зрения как оптимизации конструкций, так и скорости, наглядности и простоте получения результатов расчета с использованием современных программных комплексов. К преимуществам оболочечных расчетных моделей можно отнести следующие:
- подробный и наглядный анализ напряженно-деформированного состояния;
- точный расчет на устойчивость в пределах упругих деформаций, что особенно важно при расчетах рам на основе сварных двутавров переменного сечения;
- существенно большие возможности выполнения различных видов нелинейного анализа, и как следствие — выявление и более полное использование имеющихся резервов по несущей способности в сравнении со стержневыми моделями;
- в отдельных случаях (например, при построении расчетной модели рамы на основе двутавров переменного сечения) оболочечную модель оказывается построить быстрее, чем ее стержневую аппроксимацию стержневыми элементами постоянного сечения;
- возможность учета начальных несовершенств (например, кривизна стенки) или, при использовании объемных элементов, грибовидности фланцев в соединениях с высокопрочными преднапряженными болтами;
- оболочечные модели с применением нелинейного деформационного расчета можно применять при построении таблиц коэффициентов φ, φe, φb для профилей, отличных от нормированных в СНиП;
- следует отметить также, что иногда методики СНиП вообще не позволяют выполнить анализ несущей способности, в таких случаях альтернативы моделям с применением оболочечных, а иногда и объемных элементов просто не существует.
Для эффективного использования оболочечных элементов при расчетах стальных конструкций следует разработать и верифицировать методики построения расчетных моделей и анализа результатов, а для внедрения в проектную практику необходимы удобные и действенные средства построения расчетных моделей. Значительная часть статьи посвящена вопросам верификации результатов расчета на тестовых моделях. Для расчетов использовались программы SCAD версии 11.3 и MSC.Visual Nastran for Windows версии 2004 (далее Nastran). В качестве тестовых расчетных моделей применялись такие, расчет которых можно выполнить с применением методик СНиП II-23−81* или другой научной и технической литературы.
2. Расчет устойчивости стенок элементов двутаврового сечения в предположении упругой работы материала
С целью адекватного сопоставления с результатами расчета по СНиП II-23−81* [6] были использованы следующие положения пособия к указанному СНиП [5]:
- согласно п. 7.6, стенки балок, в которых действуют все компоненты напряженного состояния (δ, τ и δloc), рассчитываются в предположении упругой работы материала (указанное положение позволяет использовать расчет устойчивости в линейно-упругой постановке, реализованный в программе SCAD и других комплексах);
- согласно п. 7.8, устойчивость стенок балок проверяется с учетом их частичного защемления в поясах, степень которого при упругой работе балки зависит от соотношения жесткостей пояса и стенки; эффект защемления стенки поперечными ребрами жесткости не учитывается, и в местах их постановки принимается шарнирное опирание кромок (последнее положение в расчете по СНиП создает некоторый запас устойчивости, но при построении тестовых моделей не учитывалось, то есть сопряжение ребер жесткости со стенкой принято жестким);
-
согласно п. 7.8, формула (75) СНиП II-23−81*
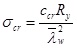 дает минимальное значение критических напряжений при чистом изгибе, которые соответствуют отношению длины отсека к его высоте a/hef=0,667; если отношение a/hef не кратно 0,667, то критические напряжения будут выше (для адекватного сравнения соотношение длины отсека к его высоте принято равным 0,667).
дает минимальное значение критических напряжений при чистом изгибе, которые соответствуют отношению длины отсека к его высоте a/hef=0,667; если отношение a/hef не кратно 0,667, то критические напряжения будут выше (для адекватного сравнения соотношение длины отсека к его высоте принято равным 0,667).
2.1. Тестовые расчеты устойчивости стенок двутавровых балок при чистом изгибе
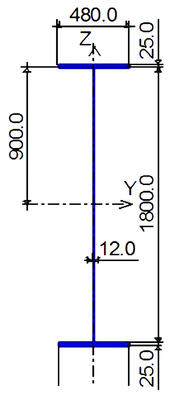
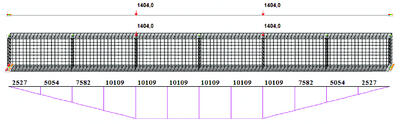
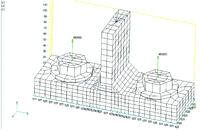
В качестве тестовой модели принята шарнирно опертая однопролетная балка пролетом 21,6 м, сечением согласно рис. 2.1.1, загруженная двумя сосредоточенными силами согласно рис.
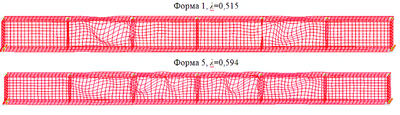
В зоне центральных отсеков стенка потеряла устойчивость по 5-й форме с коэффициентом критической нагрузки 0,594. Первая и пятая формы потери устойчивости представлены на рис.
Результаты сравнительного расчета представлены
| hefММ | hwММ | aММ |
Ry kH/см2 |
λw | λef | MkHm |
δ kH/см2 |
δcr/δ при β=∞ |
δcr/δ при β=0,8 |
Коэфф. запаса уст. SCAD |
Разница со СНиП% |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1800 | 10 | 3600 | 24 | 6,14 | 6,14 | 10108,8 | 36,62 | 0,62 | 0,593 | 0,594 | 0,15 |
| 1800 | 10 | 3600 | 24 | 5,12 | 5,12 | 10108.8 | 35,24 | 0.92 | 0,862 | 0,880 | 2,07 |
| 1800 | 14 | 3600 | 24 | 4,39 | 4,39 | 10108.8 | 33,96 | 1,3 | 1,170 | 1,199 | 2,44 |
| 1800 | 16 | 3600 | 24 | 3,84 | 3,84 | 10108.8 | 32,77 | 1,76 | 1,494 | 1,440 | 3,75 |
| 1800 | 18 | 3600 | 24 | 3,41 | 3,41 | 10108,8 | 31,66 | 2,31 | 1,952 | 1,770 | -10,27 |
Для наиболее часто используемого диапазона условных гибкостей стенок — от 4 до 6 — результаты расчета устойчивости стенки при чистом изгибе в SCAD совпадают со СНиП с точностью до 4%, что очень хорошо укладывается в общепринятую точность инженерных расчетов.
2.2. Тестовые расчеты устойчивости стенок двутавровых балок при действии преимущественно поперечной силы
Тестовая модель принята аналогично п. 2.1, но нагрузка задана в виде равномерно распределенной по оси симметрии балки, приложенной к верхнему поясу интенсивностью 130 кН/м. Расчетные модели, а также эпюры M и Q представлены на рис.
В крайнем отсеке с преобладающим внутренним усилием в виде поперечной силы стенка потеряла устойчивость по первой форме (рис. 2.2.2) с коэффициентом критической нагрузки λ=0,681.
Результаты сравнительного расчета представлены
| hefММ | twММ | λw |
δcr при β=∞ |
δcr при β=0,8 |
τcr kH/см2 |
MkHm | QkH |
δ kH/см2 |
τ kH/см2 |
КЗУ СНиП β=∞ |
КЗУ СНиП β=0,8 |
КЗУ SCAD |
Разница со СНиП% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1800 | 10 | 6,14 | 22,57 | 21,72 | 4,52 | 1158,3 | 1287 | 4,2 | 7,15 | 0,628 | 0,627 | 0,681 | 7,86 |
| 1800 | 12 | 5,12 | 32,5 | 30,37 | 6,51 | 1158,3 | 1287 | 4,04 | 5,96 | 1,082 | 1,081 | 1,110 | 2,48 |
| 1800 | 14 | 4,39 | 44,24 | 39,73 | 8,86 | 1158,3 | 1287 | 3,89 | 5,11 | 1,715 | 1,710 | 1,630 | -5,2 |
| 1800 | 16 | 3,84 | 57,78 | 48,96 | 11,57 | 1158,3 | 1287 | 3,76 | 4,47 | 2,553 | 2,540 | 2,210 | -15,54 |
| 1800 | 18 | 3,41 | 73,13 | 61,8 | 14,64 | 1158,3 | 1287 | 3,63 | 3,97 | 3,627 | 3,603 | 2,870 | -26,36 |
В таблице 2.2.1 и далее аббревиатура КЗУ означает коэффициент запаса устойчивости. В качестве КЗУ СНиП принята величина
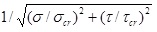
В наиболее часто используемом диапазоне условных гибкостей стенок — от 4 до 6 — результаты расчета устойчивости стенки в SCAD при превалирующем действии касательных напряжений совпадают со СНиП с точностью до 8%, что является вполне удовлетворительным показателем.
2.3. Тестовые расчеты устойчивости стенок двутавровых балок при совместном действии изгибающего момента и поперечной силы
В качестве тестовой модели принята шарнирно опертая двухпролетная балка с размером пролета 21,6 м, остальные параметры модели — как для п. 2.2. Расчетные модели, а также эпюры M и Q представлены на рис.
В отсеке у средней опоры в зоне совместного действия максимального M и Q стенка потеряла устойчивость по первой форме (рис. 2.3.2) с коэффициентом критической нагрузки λ=0,464.
Результаты сравнительного расчета представлены
| hefММ | twММ |
Ry kH/см2 |
λw |
δcr при β=∞ |
δcr при β=0,8 |
τcr kH/см2 |
MkHm | QkH |
δ kH/см2 |
τ kH/см2 |
КЗУ СНиП β=∞ |
КЗУ СНиП β=0,8 |
КЗУ SCAD |
Разница со СНиП% |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1800 | 10 | 24 | 6,14 | 22,57 | 21,72 | 4,52 | 6107,4 | 1638 | 22,12 | 9,1 | 0,447 | 0,443 | 0,464 | 4,48 |
| 1800 | 12 | 24 | 5,12 | 32,5 | 30,37 | 6,51 | 6107,4 | 1638 | 21,29 | 7,58 | 0,748 | 0,735 | 0,736 | 0,08 |
| 1800 | 14 | 24 | 4,39 | 44,24 | 39,73 | 8,85 | 6107,4 | 1638 | 20,52 | 6,5 | 1,152 | 1,115 | 1,067 | -4,45 |
| 1800 | 16 | 24 | 3,84 | 57,78 | 48,95 | 11,57 | 6107,4 | 1638 | 19,8 | 5,69 | 1,669 | 1,571 | 1,4520 | -8,2 |
| 1800 | 18 | 24 | 3,41 | 73,13 | 61,8 | 14,64 | 6107,4 | 1638 | 19,13 | 5,06 | 2,309 | 2,157 | 1,885 | -14,41 |
В наиболее часто используемом диапазоне условных гибкостей стенок от 4 до 6 результаты расчета устойчивости стенки в SCAD при совместном действии M и Q совпадают со СНиП с точностью до 5%, что укладывается в общепринятую точность инженерных расчетов.
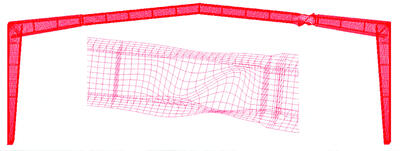
2.4. Пример расчета устойчивости стенки рамы из сварных двутавров переменной высоты
На рис.
3. Расчет несущей способности балок и рам на основе сварных двутавров переменного сечения в закритической области работы стенки
3.1. Тестовые расчеты балки с гибкой стенкой
В качестве тестовой расчетной модели была рассмотрена однопролетная шарнирно-опертая по краям балка, нагруженная равномерно распределенной нагрузкой, с сечением в виде симметричного двутавра и следующими исходными данными:
- пролет балки — 30 м;
- интенсивность нагрузки — 18,19 кН/м;
- высота сечения h=1514 мм;
- высота стенки hw=1460 мм;
- толщина стенки tw=6 мм
- толщина верхнего и нижнего поясов hf=18 мм;
- ширина верхнего и нижнего поясов bf=310 мм;
- марка стали — С245;
- шаг закреплений верхнего пояса из плоскости — от 3948 мм (в центе) до 4,28 м (ближе к краям);
- шаг односторонних поперечных ребер жесткости — от 1974 мм (два отсека в центре) до 2,14 м (остальные).
Значение момента в середине пролета M=2046 кНм.
Предельное значение момента по формуле 159 СНиП II-23−81* Mu=2231 кНм.
Результаты расчета прогибов по СНиП совместно с результатами расчета в программе Nastran приведены на рис.
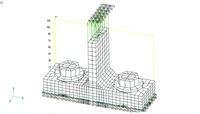
Расчет в Nastran выполнен с использованием оболочечной модели, представленной на рис.
- закрепление по каждому поперечному ребру жесткости (указанная модель в большей степени соответствует расчету по формуле 158 СНиП, поскольку не происходит потеря устойчивости по изгибно-крутильной форме);
- закрепления через поперечное ребро жесткости.
В качестве нелинейного материала использована модель упруго-пластического материала общего вида (Plastic).
Для задания функциональной зависимости между напряжениями и деформациями использовались унифицированные диаграммы работы стали в виде безразмерных напряжений и деформаций, приведенные в справочнике [3].
Вертикальные нагрузки приложены в узлах к верхнему поясу с коэффициентом 1,3 относительно расчетных, то есть 1,3*18,19=23,65 кН/м. Коэффициент 1,3 введен с целью нахождения предела несущей способности за пределами расчетной нагрузки, поскольку итерационный процесс реализуется пошагово с увеличением множителя нагрузки от 0,05 до 1. Для моделирования начальной кривизны стенки, что необходимо для корректного выполнения нелинейного расчета, перпендикулярно к стенке приложена равномерно распределенная нагрузка. При выполнении расчетов был использован нелинейный статический анализ (Nonlinear Static), позволяющий в данном случае учесть нелинейное поведение материала и влияние деформаций на изменение геометрии конструкции.
Расчеты показали, что потеря устойчивости стенки происходит при загружении балки 64% от расчетной нагрузки 18,19 кН/м, дальнейшие расчеты выполняются с выключением части стенки из силовой работы.
Для выявления момента потери несущей способности был использован метод нелинейного деформационного анализа, при котором в качестве критерия потери несущей способности принимается начало резкого роста деформаций.
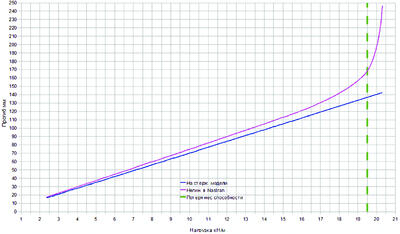
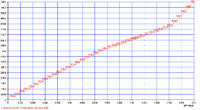
Значения нагрузок по шагам итерационного процесса и соответствующие этим нагрузкам прогибы, рассчитанные в программе Nastran, а также по стержневой модели без учета сдвиговых деформаций, но с учетом коэффициента α=0,93, рассчитанного согласно п. 18.8* СНиП II-23−81*, приведены на рис. 3.1.2 в виде графика.
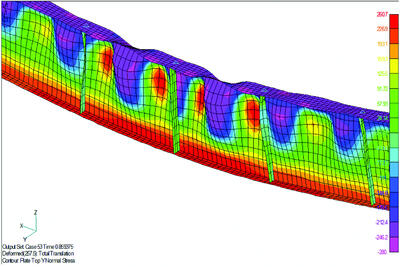
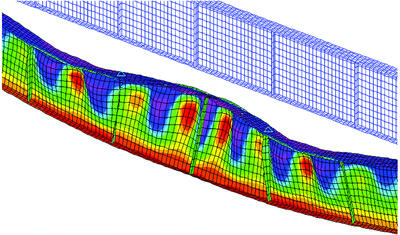
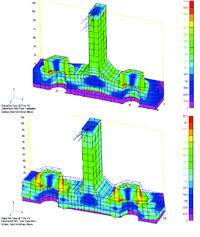
Картина напряженно-деформированного состояния центральной части балки, соответствующая шагу, принятому за момент потери несущей способности, представлена на рис.
Для модели закреплений
Выводы
Предельная нагрузка, определенная по СНиП II-23−81*:
qСНиП=qMu/M=18,19*2231/2046=19,83 кН/м.
Предельная нагрузка, рассчитанная в Nastran:
qNastran=19,508 кН/м.
Разница: 100*(19,508−19,83)/19,83=-1,62%.
Расчет в нелинейной постановке с использованием упруго-пластичной модели материала общего вида с применением унифицированной диаграммы согласно работе [3] соответствует нормативному по несущей способности с погрешностью 1,62%, что более чем достаточно для инженерных расчетов.
3.2. Тестовые расчеты центрально-сжатых стержней с применением оболочечных моделей
Согласно п. 5.7 и 5.3 пособия [5], требования по проверке устойчивости центрально-сжатых стержней установлены в СНиП II-23−81* на основе расчета внецентренно-сжатых стержней с учетом влияния формы сечения, начального искривления оси, случайного эксцентриситета сжимающей силы.
При вычислении значений коэффициентов φ типы поперечных сечений сжатых элементов принимались в соответствии с табл. 73 СНиП II-23−81*, а начальные несовершенства еb — по формуле (19) пособия [5]
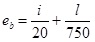 .
.
Согласно пособию [5], при нормировании коэффициентов φ определялась также критическая сила упругих идеальных стержней по методу Эйлера. Окончательные значения коэффициентов φ принимались наименьшими из двух: вычисленных с учетом начальных несовершенств или по методу Эйлера с введением коэффициента надежности λе=1,3.
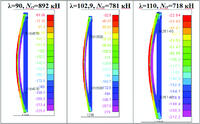
Автором были проведены расчеты стержневых моделей на устойчивость в программе SCAD и оболочечных моделей в программе Nastran как в упругой постановке (Buckling), так и в нелинейной постановке (Nonlinear Static). Известно, что при расчете на устойчивость в упругой постановке эксцентриситет приложения нагрузки не влияет на значение критической силы, расчеты оболочечных моделей на устойчивость в упругой стадии в программах SCAD и Nastran дают такие же результаты. При расчетах в программе Nastran с применением оболочечных моделей и нелинейного статического анализа (Nonlinear Static) эксцентриситет приложения нормальной силы был задан согласно методике пособия [5], а значение — по представленной выше формуле (19) пособия [5]. Расчеты были выполнены в диапазоне гибкостей от 50 до 150 для двутавра сечением 20К2 по СТО АСЧМ, что позволило исключить преждевременную потерю устойчивости стенки или поясов. Картины напряженно-деформированного состояния для гибкостей 90, 102,9 и 110 представлены на рис.
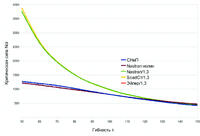
- СНиП — критическая сила, определенная по формуле (7) СНиП II-23−81* Ncr=φARy;
- Эйлер/1,3 — критическая сила, рассчитанная по формуле Эйлера с делением на 1,3;
- SCADСт/1,3 — критическая сила, рассчитанная в SCAD на стержневой модели с делением на 1,3;
- Nastran/1,3 — критическая сила, рассчитанная в Nastran на оболочечной модели в линейно-упругой постановке с делением на 1,3;
- Nastran нелин — критическая сила, рассчитанная путем выполнения нелинейного деформационного анализа на основе нелинейного статического расчета в программе Nastran.
Представленные результаты позволяют сделать следующие выводы.
-
При
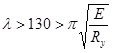 критическая сила общей потери устойчивости при решении задачи в линейной постановке с определением критической силы по формуле Эйлера на стержневой и оболочечной модели с делением на 1,3 отличается от СНиП на 6−7%.
критическая сила общей потери устойчивости при решении задачи в линейной постановке с определением критической силы по формуле Эйлера на стержневой и оболочечной модели с делением на 1,3 отличается от СНиП на 6−7%.
- В диапазоне рабочих гибкостей колонн от 80 до 120 расчет в линейной постановке дает погрешность от 70 до 30% (без учета коэффициента 1,3). В указанном диапазоне нелинейный деформационный анализ совпадает со СНиП в пределах 5%, что является достаточным для инженерных расчетов.
-
При
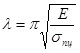 , критическая сила, определенная на оболочечной модели путем нелинейного деформационного анализа, полностью совпадает с критической силой, определенной по СНиП.
, критическая сила, определенная на оболочечной модели путем нелинейного деформационного анализа, полностью совпадает с критической силой, определенной по СНиП.
- Таким образом, при гибкостях более 130 расчет на устойчивость при центральном сжатии с применением оболочечной модели следует выполнять в линейной постановке с использованием коэффициента надежности 1,3.
- При гибкостях от 110 до 130 оболочечные модели для расчета устойчивости при центральном сжатии можно применять, только выполняя нелинейный деформационный анализ на основе нелинейного статического расчета, при этом дополнительный коэффициенты запаса можно принимать не более 5%.
- При гибкостях менее 110 оболочечные модели для расчета устойчивости при центральном сжатии можно применять, только выполняя нелинейный деформационный анализ на основе нелинейного статического расчета, при этом дополнительный коэффициенты надежности не нужны.
3.3. Пример расчета рамы с учетом закритической работы стенки
Представленные в п. 3.1. и 3.2. результаты тестовых расчетов подтверждают хорошую сходимость моделей на оболочечных элементах при нелинейном статическом расчете в Nastran с расчетом по СНиП, что позволяет применять разработанную методику для оценки несущей способности рамных конструкций на основе сварных двутавров переменного сечения с учетом в закритической области работы стенки.
На рис.
4. Применение объемных элементов при расчете фланцевых соединений на высокопрочных болтах с предварительным натяжением
4.1. Проблемы, возникающие при производстве стальных конструкций с применением фланцевых соединений
При производстве стальных конструкций с применением фланцевых стыков на высокопрочных преднапряженных болтах во фланцах часто возникают остаточные деформации в форме грибовидности.
Существующие рекомендации, разработанные ЦНИИПСК в 1989 г., предъявляют жесткие требования к изготовлению фланцев, которые зачастую могут быть выполнены только с применением дорогостоящей операции фрезеровки поверхности фланца, что на практике выполняется не каждым производителем. Указанные требования имеют обоснование, поскольку деформации фланца приводят к существенному увеличению доли внешней нагрузки на болты вследствие потери натяжения на преодоление начальных остаточных деформаций фланца, а в 1989 году не было таких расчетных возможностей, какие предоставляют современные программные комплексы.
Согласно данным монографии [2], грибовидность фланцев не влияет на их несущую способность при допущении пластических деформаций, но оказывает влияние на распределение усилий в преднапряженных высокопрочных болтах и на долю внешней нагрузки, передаваемой на болты, что может привести к их разрушению, потере несущей способности соединения и обрушению конструкции.
На принятие решения о пригодности к эксплуатации конструкций с дефектами во фланцах или о способах их доработки в современных условиях, при жестких сроках на изготовление и поставку стальных конструкций, должно уходить не более 1−2 дней. Такие сроки принятия решений вполне возможны при наличии подробной расчетной модели фланцевого стыка без учета остаточных деформаций, а также наличии технологии расчета с учетом остаточных деформаций. Далее представлены контуры такой технологии на примере расчета тестовых моделей Т-образного фланца.
4.2. Тестовые модели Т-образных фланцев на основе объемных конечных элементов
Тестовая расчетная модель Т-образного фланца без дефектов, с нагрузкой, приложенной по оси болта, выполненная в программе Nastran, приведена на рис.
График, приведенный на рис. 4.2.2, имеет следующие характерные точки:
- осевое напряжение в стержне болта, равное 53,12 кН/см2, при SetValue=1 соответствует окончанию пошагового приложения нагрузки от предварительного натяжения N=53,12*4,524=240,31 кН, где 4,524 см2 — площадь нетто болта диаметром 24 мм;
- далее, от точки с осевым напряжением 53,12 кН/см2 при SetValue=1 до точки с осевым напряжением 801,2 кН/см2 при SetValue=1,75, участок графика соответствует приложению внешней нагрузки от 0 до 0,75*480=360 кН, при которой происходит раскрытие фланца и передача всей последующей нагрузки на болты;
- точка, при SetValue=2, с осевым напряжением 106,1 кН/см2, соответствует приложению всей внешней нагрузки N=106,1*4,524=480 кН, принятой в два раза больше несущей способности примыкающего к фланцу участка пояса.
Анализ графика, приведенного на рис. 4.2.2, показывает, что от начала приложения нагрузки до момента раскрытия фланца болтом воспринято 34% от внешней нагрузки. Согласно данным монографии [2], для аналогичного соединения коэффициент внешней нагрузки для высокопрочных болтов диаметром 24 мм χ=0,157, что почти в 2,17 раза меньше полученных результатов. Указанная разница, очевидно, вызвана тем, что в расчетной модели не учтен ряд факторов, влияющих на податливость системы болт — гайка — шайба, например, податливость резьбы и разность податливости нарезной и ненарезной частей стержня болта. Неучтенные в расчетной модели факторы, влияющие на податливость, можно учесть, меняя диаметр или модуль упругости стержневого элемента, моделирующего болт, при выполнении настройки методики для применения в практических расчетах. Аналогично можно придумать способ построения модели без подробного моделирования головки болта и шайбы. Для определения эквивалентного диаметра стержневого элемента необходимо применить модель, соответствующую модели в виде конуса, которая была использована в монографии [2] для получения коэффициента внешней нагрузки, а также сопоставить результаты расчета с экспериментальными данными.
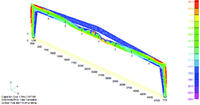
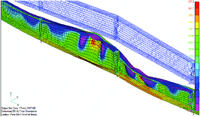
Далее представлены результаты расчета фланцев с нагрузкой, приложенной к соединенному с фланцем участку пояса толщиной 16 мм (рис. 4.2.3) для идеального фланца и фланца с грибовидностью в форме выпуклости вверх. Для участка пояса и стержня болта материал линейно-упругий. Для фланца, сварного шва, головки болта и шайбы — упруго-пластический билинейный (Elasto-Plastic (Bi-Linear)). Расчет выполнен в нелинейной постановке (Nonlinear Static). Для создания грибовидности написана программа, пересчитывающая координаты узлов по деформациям, вызванным специально заданным загружением. Проблема задания параметров начального раскрытия элемента (Initial Gap) в элементах односторонней связи Gap, которая меняется от 0 по краям фланца до максимального 0,5 мм в центре фланца, также решена с помощью специально написанной программы. На рис. 4.2.3−4.2.6 представлены результаты расчета идеального и грибовидного фланцев.
Анализ представленных выше графиков показывает, что несущая способность фланца исчерпывается при 80% внешней нагрузки, принятой по резкому росту перемещений.
Анализ осевых напряжений в болтах свидетельствует, что при 80% внешней нагрузки в модели с грибовидностью их значение составляет 90,64 кН/см2, а в модели без грибовидности — 79,76 кН/см2. При расчетном сопротивлении стержня болта 77 кН/см2 для фланца без грибовидности разрушение по болтам происходит при 77% от номинальной внешней нагрузки, а с грибовидностью — при 62%. При этом следует отметить, что несущая способность пояса исчерпывается при 50% номинальной нагрузки, то есть для фланца с грибовидностью запас несущей способности по болтам составляет 12% относительно несущей способности пояса. В приведенной модели параметры фланца и грибовидности были взяты из реальной ситуации, с которой пришлось столкнуться автору, что подтверждает целесообразность выполнения подобных расчетов для принятия решения о возможности эксплуатации фланцевого соединения с деформациями фланцев в форме грибовидности или о необходимости их усиления. Очевидно, что описанная методика подходит и для расчета усиления соединения и вполне может применяться заводами-изготовителями металлоконструкций для обоснования отказа от трудоемких и затратных операций по фрезеровке фланцев.
Литература
- Вычислительный комплекс SCAD /
В.С. Карпиловский ,Э.З. Криксунов ,А.А. Маляренко ,М.А. Микитаренко ,А.В. Перельмутер ,М.А. Перельмутер , — М.: СКАД СОФТ, 2009. - Катюшин
В.В. Здания с каркасами из стальных рам переменного сечения (расчет, проектирование строительство), — М.: Стройиздат, 2005. - Кузнецов
В.В. Металлические конструкции. — В 3 т.; Т. 1. Общая часть. (Справочник проектировщика) / Под общ. ред. засл. строителя РФ, лауреата гос. премии СССРВ.В. Кузнецова (ЦНИИпроектстальконструкция им. Н.П. Мельникова). — М.: АСВ. 1998. - Рычков С.П. MSC.visualNastran для Windows М.:
НТ Пресс , 2004. - Пособие по проектированию стальных конструкций (к СНиП II-23−81* «Стальные конструкции») / ЦНИИСК им. Кучеренко Госстроя СССР. — М.: ЦИТП Госстроя СССР, 1989.
- СНиП II-23−81*. Стальные конструкции. — М.: ЦПП, 2008.
Скачать статью в формате PDF — 573.0 Кбайт |