Вернуться к версии для экрана CADmaster » Выпуски » CADmaster #5(40) 2007

Реализация в программном комплексе SCAD блочного метода Ланцоша со сдвигами применительно к сейсмическому анализу сооружений

Введение

При решении задач сейсмического анализа зданий и сооружений чаще всего применяется линейно-спектральный метод. Значительной по трудоемкости составляющей этого подхода является определение частот и форм собственных колебаний. При этом возникает вопрос:, а сколько частот и форм собственных колебаний следует удерживать, чтобы результат был достоверным? В сейсмических нормах многих стран (Еврокод 8, UBC-97, сейсмические нормы Украины и др.) принято, что сумма модальных масс по каждому из направлений сейсмического воздействия должна быть не менее установленной границы. Обычно для горизонтальной составляющей сейсмического воздействия принимается 85–90%, для вертикальной – 70–90%. Под направлением сейсмического воздействия понимается направление, совпадающее с одной из осей глобальной системы координат OXYZ расчетной модели сооружения. Считается, что сейсмическое воздействие поочередно прикладывается вдоль каждой оси, причем принимается гипотеза об их статистической независимости [5, 8].

Модальной массой при сейсмическом воздействии в направлении dir (dir = OX, OY, OZ) называется величина

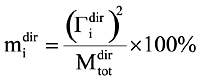
, где Г_i^dir = (Mψ_i, I_dir), M – матрица масс, ψ_i – собственный вектор (форма колебаний, отвечающая i-й частоте), I_dir – вектор, компоненты которого равны 1, если соответствуют степени свободы сейсмического входа по направлению dir, и нулю в противном случае,

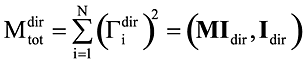
– общая масса, участвующая в движении по направлению dir.

Суммой модальных масс по направлению dir называется величина 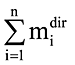, причем

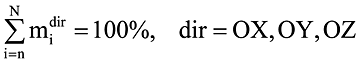
, где N – количество степеней свободы дискретной модели [3, 5, 8], n – количество удерживаемых собственных форм, n < < N.

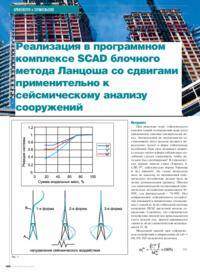
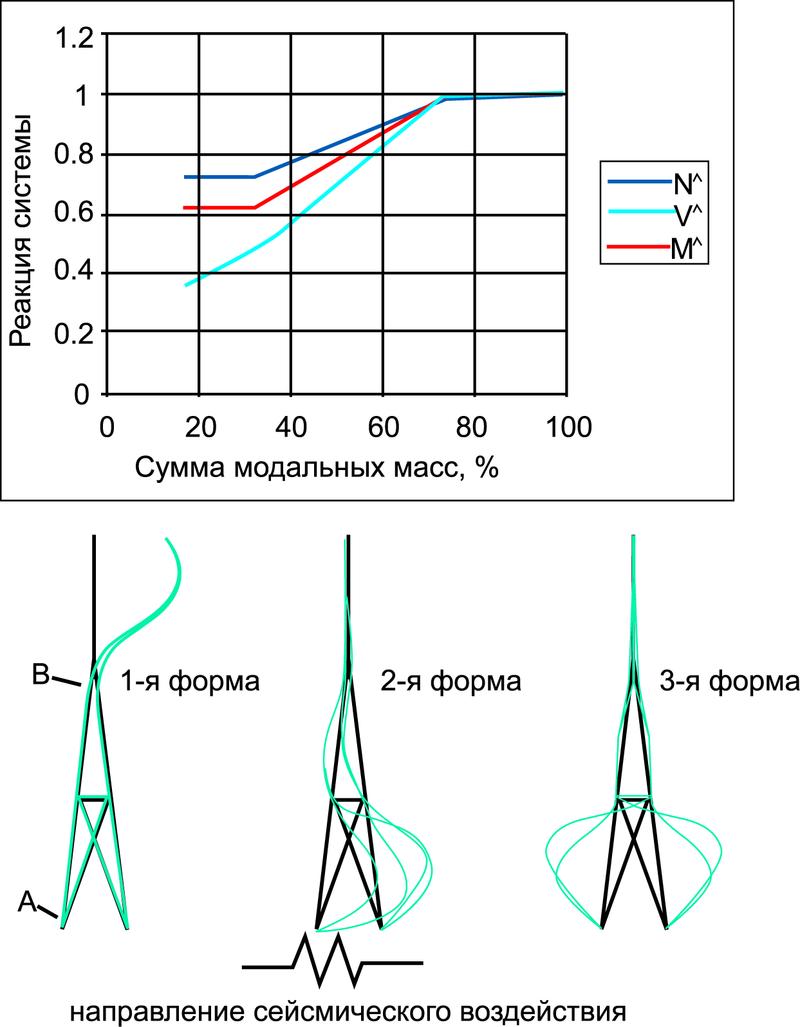
В [3] на примере простой задачи показана зависимость некоторых внутренних усилий от суммы модальных масс (рис. 1).

Рис. 1

Здесь N^Λ = N_A ⁄ N_A¹⁰⁰; V^Λ = V ⁄ V¹⁰⁰; M^Λ = M_ov ⁄ M_ov¹⁰⁰, N_A – продольная сила в стержне А, V – суммарная сдвигающая сила в основании, M_ov – опрокидывающий момент. Символ ¹⁰⁰ означает, что этот фактор получен при удержании в решении всех собственных форм дискретной модели (100% модальных масс).

Рис. 1 иллюстрирует тот факт, что для получения достоверной сейсмической реакции сооружения необходимо удерживать такое количество собственных форм, чтобы обеспечить высокий процент модальных масс (не менее 80%). При этом, разумеется, расчетная модель должна достаточно достоверно описывать поведение системы.

Таким образом, сумма модальных масс в сейсмическом анализе используется как индикатор достаточного количества удерживаемых форм колебаний.

При решении ряда задач было обнаружено, что суммы модальных масс сходятся крайне неравномерно и очень медленно [2]. При работе с расчетными моделями, содержащими большое количество степеней свободы (несколько сот тысяч), возникает серьезная проблема определения большого количества частот и форм собственных колебаний (порядка нескольких тысяч), представляющая собой сложную вычислительную задачу.

В этой работе представлен один из методов решения – блочный метод Ланцоша со сдвигами, реализованный автором в программном комплексе SCAD.

Блочный метод Ланцоша со сдвигами

В основу этой статьи положена работа Р. Граймса, Дж. Льюиса и Г. Саймона «A shifted block Lanczos algorithm for solving sparse symmetric generalized eigenproblems» [7]. Алгоритм данной реализации метода приведен в [4], а ее внедрение в программный комплекс SCAD представлено в [1]. Отметим, что блочная версия алгоритма позволяет сократить медленные операции ввода-вывода по сравнению с классической (неблочной) версией. Введение сдвигов существенно улучшает сходимость, а в случае определения большого количества собственных пар разделяет длинный частотный интервал на относительно короткие подинтервалы, ограничивая тем самым размерность пространства Крылова и заменяя экспоненциальный рост количества вычислений квазилинейным. Если исходная задача на собственные значения представляется как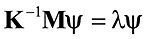 

, где K, M – соответственно положительно определенная разреженная матрица жесткости и полуопределенная матрица масс, {λ, ψ} – собственная пара. Вводя сдвиги σ₁, σ₂,…, σ_k, разбиваем этот частотный интервал на к+1 подинтервалов, на каждом из которых решаем задачу

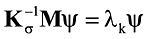
где K_σ = K — σ_kM, λ_k = 1 ⁄ (ω² — σ_k).

Таким образом, на каждом частотном подинтервале решается отдельная задача (4). Алгоритм выглядит так: при отсутствии какой-либо информации о спектре собственных частот полагаем σ₁ = 0 . Затем выполняем L шагов блочного метода Ланцоша и определяем сошедшиеся собственные пары. Далее анализируется сумма модальных масс для сошедшихся собственных пар. Если хотя бы по одному из направлений сейсмического входа сумма модальных масс меньше указанной, осуществляется переход к новому частотному интервалу. Кроме сошедшихся собственных пар имеются приближения собственных частот, которые еще не сошлись. Именно они используются для прогнозирования нового значения параметра сдвига σ₂ . Приняв сдвиг на основе такого прогноза, продолжаем вычисления на новом частотном интервале до тех пор, пока не определим все собственные числа, лежащие слева от сдвига и справа от последнего собственного числа, соответствующего сошедшейся собственной паре с предыдущего частотного интервала. Затем снова определяем суммы модальных масс. И так до тех пор, пока не будет достигнута достаточная сумма модальных масс.

Пример расчета

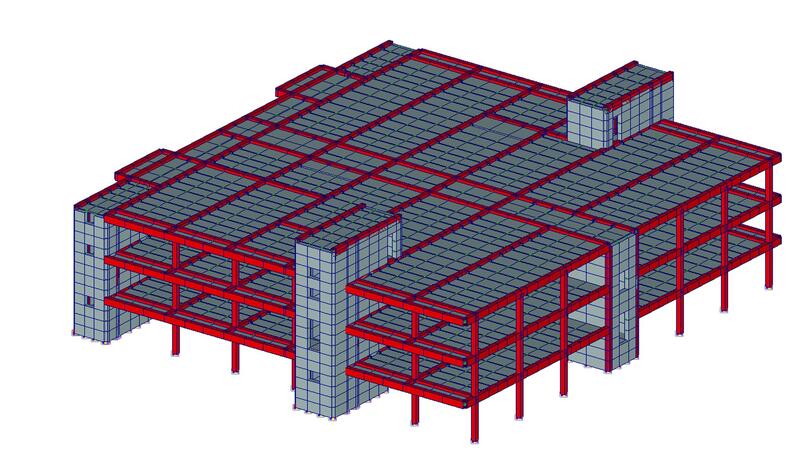
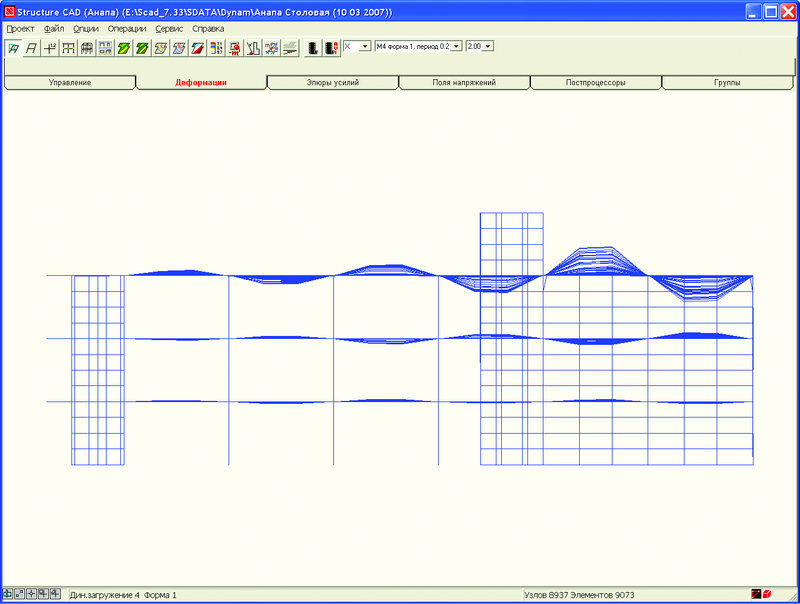
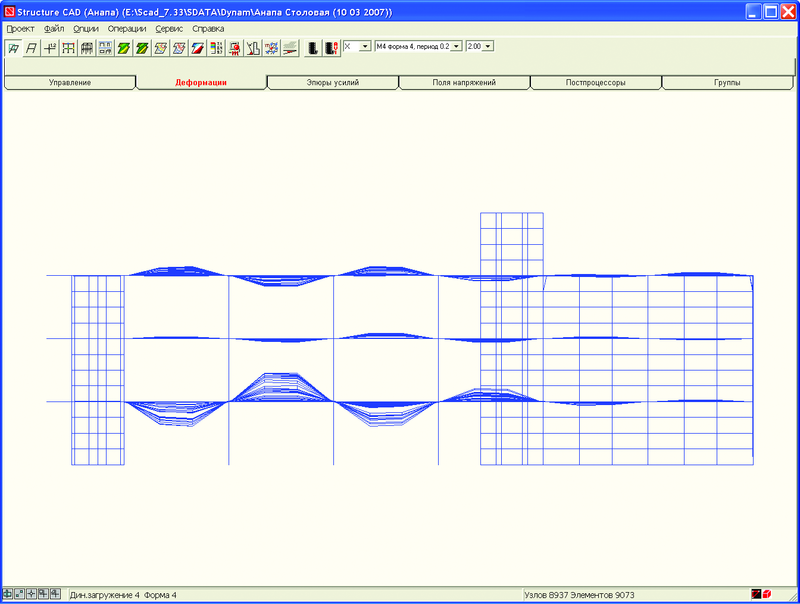
На рис. 2 приведена расчетная модель здания, включающая 8937 узлов, 9073 конечных элементов и 52 572 уравнения.

Рис. 2. Расчетная модель здания

По количеству уравнений эта задача на сегодняшний день относится к классу средних, однако по сложности решения обобщенной проблемы собственных значений она очень трудна, так как вследствие значительной жесткости несущих конструкций в нижней части спектра расположены локальные формы колебаний (рис. 3, 4), и только форма колебаний, соответствующая 522-й частоте (рис. 5), существенно влияет на сейсмическую реакцию сооружения (m₅₂₂^ox = 29% , тогда как ).

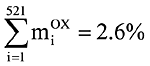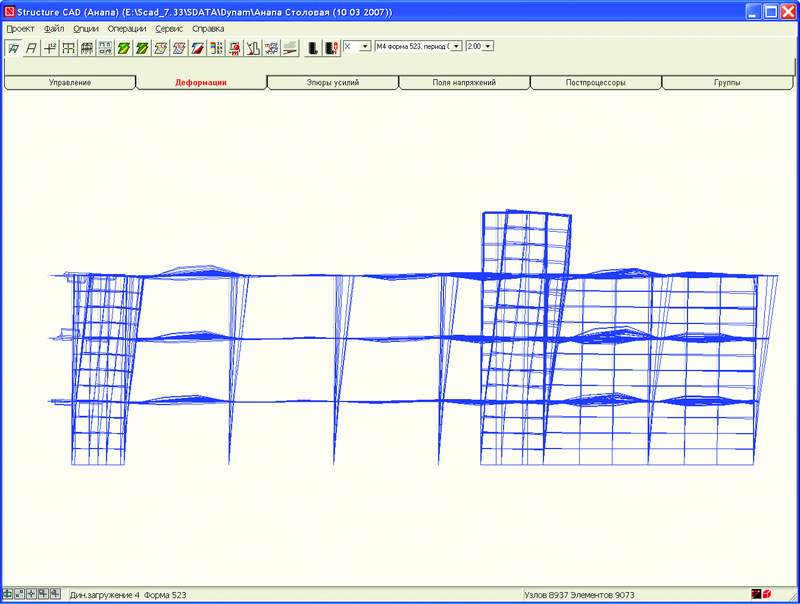
Наибольший вклад дает 523-я форма колебаний, представленная на рис. 5.

Рис. 5.523-я форма колебаний, частота 5,756 Гц

Для обеспечения требуемых сумм модальных масс пришлось определить 2398 собственных пар.

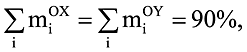
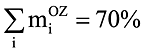
Спектр собственных частот для этой задачи очень густой – в интервале [4.183, 5.756] Гц лежит 523 собственных частоты.
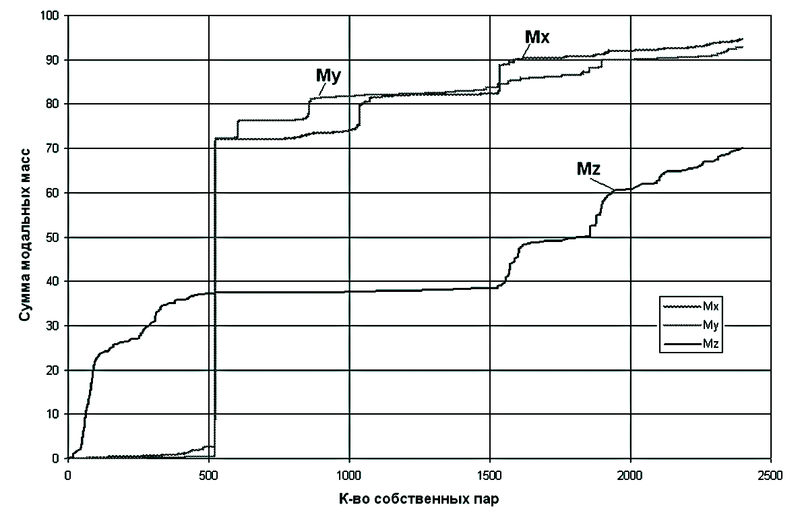
Зависимость сумм модальных масс от количества удерживаемых собственных форм приведена на рис. 6.

Рис. 6. Зависимость сумм модальных масс (Mx, My, Mz) от количества удерживаемых собственных форм

Выводы

При расчетах зданий и сооружений на сейсмику периодически встречаются задачи, в которых в нижней части спектра лежит большое количество локальных форм колебаний, причем спектр собственных частот является очень густым. Такие задачи создают серьезные проблемы, поскольку вычислительные алгоритмы, реализованные в современных компьютерных системах МКЭ-анализа, как правило, в таких случаях оказываются малоэффективными. Разработанный в программном комплексе SCAD алгоритм блочного метода Ланцоша со сдвигами, реализующий сейсмический режим, позволяет значительно продвинуться в решении этой проблемы.

Литература

1. Карпиловский В.С., Криксунов Э.З., Фиалко С.Ю. Блочный метод Ланцоша со спектральными трансформациями для решения больших МКЭ задач собственных колебаний. – Вісник Одеського національного морського університету. – 2003, №10, с. 93–99.
2. Перельмутер А.В., Карпиловский В.С., Фиалко С.Ю., Егупов К.В. Опыт реализации проекта МСН СНГ «Строительство в сейсмических районах» в программной системе SCAD. – Вісник Одеської державної академії будівництва та архітектури. – 2003, випуск 9, с. 147–159.
3. Фиалко С.Ю. Некоторые особенности анализа частот и форм собственных колебаний при расчете сооружений на сейсмические воздействия. – Вісник Одеської державної академії будівництва та архітектури. – 2002, випуск 8, с. 193–201.
4. Фиалко С.Ю. О решении обобщенной проблемы собственных значений. – В кн. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. – Издание второе. К.: Сталь, 2002, с. 570–597.
5. Clough R., Penzien J. Dynamics of structures. – New York: McGraw-Hill, Inc., 1975. – 527 p.
6. Fialko S.Yu., Kriksunov E.Z. and Karpilovskyy V.S. A block Lanczos method with spectral transformations for natural vibrations and seismic analysis of large structures in SCAD software. Proceedings of the CMM-2003 – Computer Methods in Mechanics, June 3–6, 2003. Gliwice, Poland, р. 129–130.
7. Grimes R.G., Lewis J.G., Simon H.D. A shifted block Lanczos algorithm for solving sparse symmetric generalized eigenproblems. SIAM J. Matrix Anal. Appl. V.15, 1: pp.1–45, 1994.
8. Wilson E.L. Three dimensional dynamic analysis of structures. California, Computers and Structures, Inc., Berkeley, USA, 1996. – 261 p.