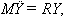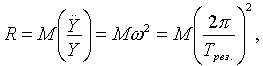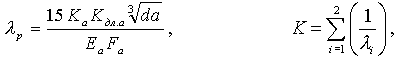CADmaster

Поскольку учет свойств реальной конструкции возможен лишь с определенной степенью приближения, одной из важных и первоочередных задач при создании математической модели несущей конструкции с использованием современного вычислительного комплекса является возможность ввода в эту модель тех параметров и свойств, которые позволяют обосновать результаты натурных экспериментов. В статье изложен способ построения конечно-элементной модели фрагмента безригельного каркаса по результатам его вибрационных испытаний. Расчеты были выполнены в ВК SCAD Office. Регулирование обобщенной жесткости фрагмента позволило добиться максимального совпадения с экспериментальными данными.

Основные результаты вибрационных испытаний

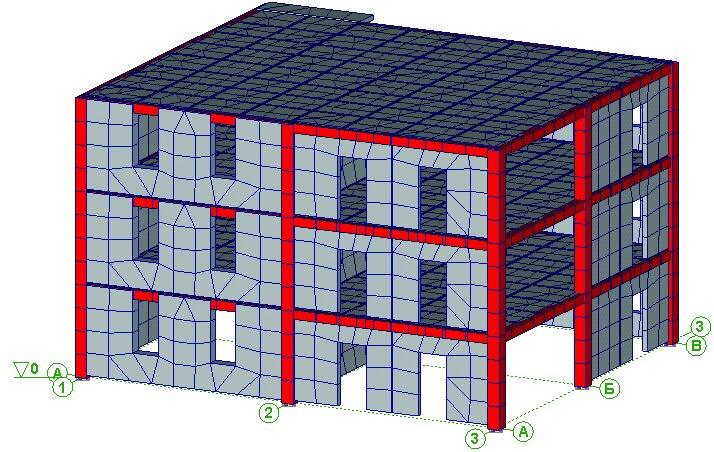
Опытный объект представляет собой трехэтажный фрагмент безригельного каркаса серии 1.120с, смонтированного с применением предварительного напряжения высокопрочных канатов.

Фрагмент состоит из четырех конструктивных ячеек размером 7,2×6 м и имеет ширину 12 м и длину 14,4 м; высота этажа составляет 3 м (рис. 1). Трехэтажный фрагмент установлен на фундаментной плите-ростверке и имеет свайное основание. Для передачи горизонтальной статической нагрузки на каркас фрагмента на фундаментной плите с размерами 15×30 м с обеих сторон возведены из монолитного железобетона стены-упоры высотой 9 м. Фрагмент рассчитан и запроектирован на 8-балльные сейсмические нагрузки. Масса фрагмента с учетом дополнительного пригруза составила на момент проведения испытаний 420 тонн. Начальные значения периода собственных колебаний неповрежденного фрагмента по записям микросейсм составили 0,17 — 0,19 с. Заполнение каркаса выполнено с применением кирпичной кладки и мелких блоков из ячеистого бетона неавтоклавного твердения.

Сейсмостойкость безригельного каркаса обеспечивается в основном за счет работы железобетонных диафрагм жесткости. Как показали испытания, обжатие элементов перекрытия высокопрочными канатами сыграло значительную роль в обеспечении пространственной неизменяемости и устойчивости фрагмента.

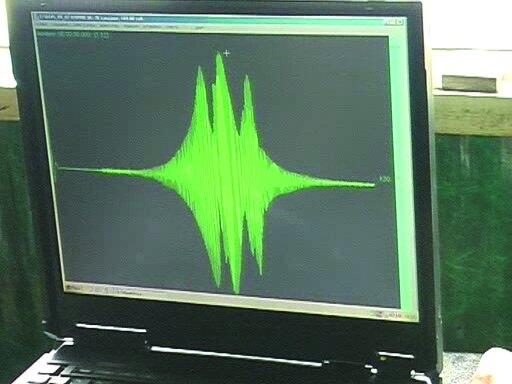
Сущность вибрационных испытаний заключается в плавном прохождении зоны резонанса при увеличении числа оборотов электропривода — «прямой резонанс». При дальнейшем увеличении числа оборотов привода система «опытный объект + вибромашина» уходит за первый резонанс и достигает последующих резонансных зон. При уменьшении числа оборотов привода в системе наблюдается «обратный резонанс», частота которого может отличаться от частоты прямого резонанса за счет накопления повреждений. Интенсивность вибрационного нагружения регулируется числом сблокированных вибраторов и количеством грузов-дебалансов на их рычагах. Внешняя сила, создаваемая вибромашиной, изменяется по гармоническому закону [1]. В качестве примера на рис. 2 показан график ускорений при прохождении резонансной зоны на одном из каналов 36-канальной сейсмометрической станции, с помощью которой велась запись кинематических параметров в процессе испытаний. При чтении развертки слева направо: вначале зарегистрирован первый резонанс в прямом направлении, затем идет второй пик ускорений, который соответствует второму резонансу, и, наконец, третий пик означает прохождение зоны первого резонанса в обратном направлении на выбеге вибромашины.

В начале испытаний фрагмент был подвергнут воздействию двух вибромашин, установленных на фундаментной плите и включаемых раздельно в продольном и поперечном направлениях. Максимальные значения ускорений составили на фундаментной плите 0,1 g, на покрытии — 0,2 g. Периоды резонансных колебаний фрагмента 0,20 — 0,22 с.

Затем к фрагменту были приложены статические знакопеременные нагрузки в продольном направлении в уровне покрытия с помощью двух 100-тонных домкратов ДГ-100/300. Суммарная горизонтальная нагрузка составила 2000 кН. Нагружение велось этапами по 290 кН с выдержкой 10 мин. Максимальные перемещения в уровне покрытия составили 19 мм; максимальный перекос третьего этажа — 6 мм. Всего было проведено три цикла нагружения: два цикла справа и один слева.

Далее одна из вибромашин была переставлена на покрытие и проведены вибрационные испытания фрагмента в поперечном направлении. Значения периодов резонансных колебаний: начальное — 0,20 с, конечное — 0,44 с, что эквивалентно уменьшению обобщенной жесткости вследствие накопления повреждений в 4,8 раза. Максимальные ускорения на покрытии составили 0,82 g, в уровне фундаментной плиты — 0,20 g. Максимальное значение амплитуды колебаний в уровне покрытия 31 мм; суммарная инерционная нагрузка достигла 2000 кН при расчетной величине 8-балльной нагрузки 420 кН.

Следующий этап статических испытаний фрагмента в продольном направлении проводился с помощью двух 200-тонных домкратов ДГ-200/150. Суммарная горизонтальная нагрузка достигла 4000 кН. Нагружение велось этапами по 580 кН с выдержкой 5−10 мин. Максимальные перемещения в уровне покрытия составили 115 мм; максимальный перекос третьего этажа — 65 мм. Всего было проведено четыре цикла нагружения по два цикла справа и слева.

На заключительном этапе испытаний фрагмент был подвергнут вибрационному нагружению в продольном направлении. Значения периодов резонансных колебаний: начальное — 0,22 с, конечное — 0,45 с; обобщенная жесткость фрагмента уменьшилась в 4,2 раза. Максимальные ускорения на покрытии составили 0,82 g, в уровне фундаментной плиты — 0,20 g. Максимальное значение амплитуды колебаний в уровне покрытия 50 мм; суммарная инерционная нагрузка превысила 2700 кН. Приближенно сейсмическая нагрузка при реальных 8-балльных воздействиях может быть оценена по формуле S = S_p ⁄ K₁,
где S_p — расчетная сейсмическая нагрузка согласно СНиП II-7−81*,
К₁ — коэффициент допускаемых повреждений (коэффициент редукции). Реальная сейсмическая нагрузка для 8 баллов составляет S = 420⁄0,25 = 1680 кН. Достигнутая в процессе испытаний инерционная нагрузка превышает этот уровень в 1,6 раза (2700/1680). В результате испытаний фрагмент был доведен до предельного состояния.

Выполненный на основании экспериментальных данных анализ механизма перехода сооружений в предельное состояние [2] позволил вскрыть последовательность образования в конструкциях и узлах фрагмента зон развития неупругих деформаций и повреждений, а также выявить особенности их поведения при динамических нагрузках (эта информация была использована при построении КЭ-модели). К их числу относятся:

• разрушения заделки колонн в фундаментах стаканного типа по осям 1 и 3, которые послужили причиной вертикальных колебаний фрагмента;
• массовые повреждения шпонок в диафрагмах жесткости;
• значительные повреждения и частичное обрушение стенового заполнения из мелких блоков;
• расстройство стыков колонн «штепсельного» типа в уровне перекрытия над первым этажом;
• вертикальные колебания перекрытия с амплитудой 5 мм на частоте 7−8 Гц в зоне установки вибромашины.

В силу этого фрагмент работает как существенно нелинейная нестационарная система. Причем нестационарность системы обусловлена как изменением частотных, так и диссипативных характеристик сооружения.

Для дальнейшего анализа важно отметить, что основные повреждения, которые привели к деградации обобщенной жесткости фрагмента, в основном были сосредоточены в узлах соединения элементов: диафрагм жесткости, колонн и элементов перекрытия, а также (в меньшей степени) заполнении каркаса фрагмента. Жесткость самих элементов, несмотря на развитие в них трещин в процессе динамического и статического знакопеременного нагружения, уменьшилась незначительно.

Физическая модель фрагмента

Сущность приближенного способа построения физической модели фрагмента заключается в замене исходной нелинейной нестационарной системы последовательностью линейно-упругих одномассовых систем, частоты которых соответствуют резонансным частотам основной формы собственных колебаний, зарегистрированные при различном уровне динамического нагружения. В работе [1], в которой использован аналогичный подход, такие системы названы «условными линейными диссипативно-нестационарными системами». Применение моделей в виде одномассового осциллятора оправдано тем, что фактически подбор жесткостных параметров модели производился только с учетом первой формы собственных колебаний.

Как известно, в момент резонанса для одномассовой системы [3]:

• упругая сила R_у уравновешивает силу инерции системы J;
• внешняя сила P = P₀Sin(ωt), создаваемая вибромашиной, где ω — круговая частота, уравновешивается силой затухания R_ε;
• векторы всех сил сдвинуты по фазе по отношению друг к другу на угол π⁄2.

Отсюда следуют два равенства:

J = R_у и Р = R_ε.

Раскрывая первое равенство, получим

где М и R — обобщенная масса и обобщенная жесткость системы, Y — вектор перемещений.

Обобщенная жесткость может быть найдена по формуле

где T_рез. — период резонансных колебаний; обобщенная масса системы сосредоточена в уровне η = 1, где η — коэффициент формы колебаний.

Обобщенная масса системы определяется расчетным путем по формуле

М = ∑m_iη_ik²,

где m_i — поэтажные сосредоточенные массы.

Периоды резонансных колебаний определены экспериментальным путем на различных этапах вибрационных испытаний с точностью до ±0,01 с и представлены в таблице 1.

Таблица 1. Экспериментальные значения резонансных колебаний фрагмента на различных этапах вибрационных испытаний

Наименование	Этапы вибрационных испытаний
	1	2	3	4	5	6	7	8
Периоды резонансных колебаний, с	0,22	0,24	0,26	0,32	0,34	0,38	0,40	0,45
Ускорения в уровне η = 1, м/с2	0,68	1,87	4,04	6,18	6,65	6,86	7,73	8,05
Инерционная нагрузка, кН	230	640	1374	2101	2261	2332	2628	2737
Обобщенная жесткость фрагмента, 10-3 кН/м	277	233	198	131	116	93	84	66

Использование вычислительного комплекса SCAD Office при формировании расчетной модели

Конечно-элементная модель (КЭ-модель) фрагмента сформирована с помощью препроцессора ФОРУМ с импортированием исходной графической информации из системы AutoCAD [4]. При моделировании стержневых и пластинчатых конструктивных элементов фрагмента были использованы конечные элементы типа «пространственный стержень» и КЭ из группы оболочечных элементов. Количество узлов расчетной схемы — 2525, количество элементов — 4073. Число степеней свободы (число активных масс) — 7536, порядок системы линейных уравнений — 15102.

Таблица 2. Интервалы изменения жесткостей специальных КЭ в масштабе 10^-3 кН⁄м

Наименование		Номера конечных элементов
		51	55
			Диафрагмы жесткости	Кирпичное заполнение	Мелкие блоки
Начальные значения (Трез. = 0,22 с)	оси X, Y	50	50	20	10
	ось Z	35	200	200	200
Конечные значения (Трез. = 0,45 с)	оси X, Y	2,5	5	5	5
	ось Z	2,5	10	10	10

Для описания работы узловых соединений конструктивных элементов фрагмента с фундаментной плитой использован специальный конечный элемент КЭ № 51 — связь конечной жесткости [5]. Для всех остальных узлов соединения фрагмента также применен специальный КЭ № 55 — упругая связь между узлами. Регулирование обобщенной жесткости фрагмента в процессе построения последовательности линейно-упругих моделей, описывающей поведение нелинейной нестационарной системы, осуществлялось за счет изменения жесткостных характеристик указанных специальных конечных элементов № 51 и № 55. Жесткости всех остальных конечных элементов моделей полагались постоянными. Начальные и конечные значения жесткостей для указанных КЭ представлены в таблице 2.

По своей конструкции узлы соединения диафрагм жесткости с фундаментной плитой и элементами перекрытий представляют собой шпонки, армированные двумя арматурными выпусками диаметром Ø14AIII и замоноличенные бетоном класса В20. Податливость одной арматурной связи λ_р и жесткость всего соединения К могут быть оценены с помощью формул (5 и 3) ВСН 32−77 [6]:

где К_а — коэффициент, зависящий от вида арматурной стали выпусков;
К_а = 1 для стержней периодического профиля;
К_дл.а — коэффициент, учитывающий длительность растяжения стыкового соединения;
К_дл.а = 1 при кратковременном растяжении;
d_а = 1,4 — диаметр арматурной связи;
Е_а, F_a — модуль упругости и площадь сечения арматурной связи в кг/см2 и см2.

Вычисления по этим формулам дали следующие результаты: λ_р = 0,26×10^-3 см/кН, К = 385×10³ кН/м. Как видим, полученная жесткость одного узла соединения в 2−10 раз превышает начальные значения жесткостей по оси Z соответственно для КЭ № 55 и КЭ № 51 (таблица 2), что объясняется высоким уровнем динамических воздействий в процессе испытаний фрагмента.

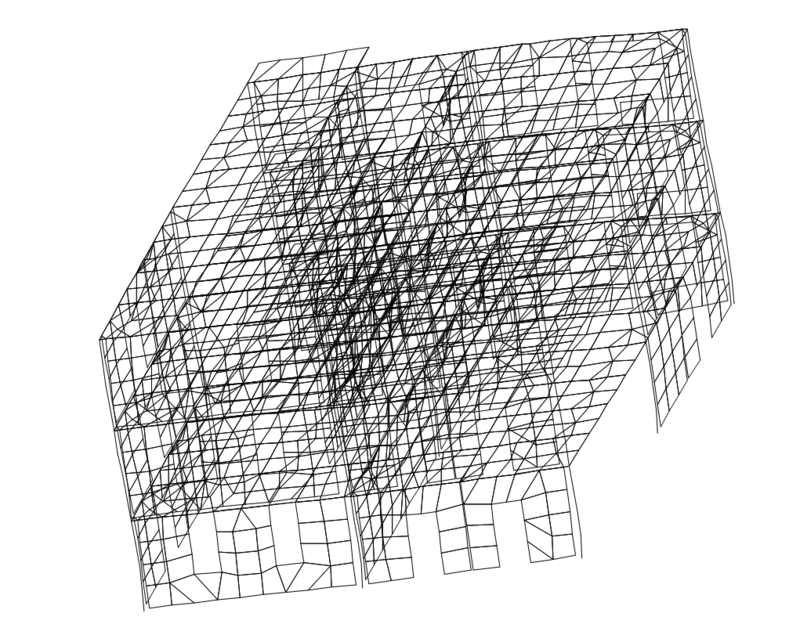
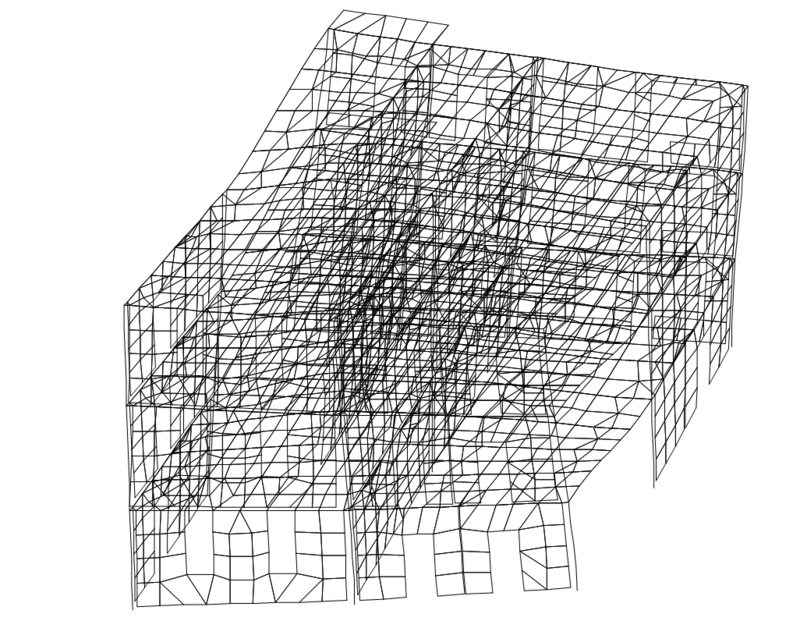
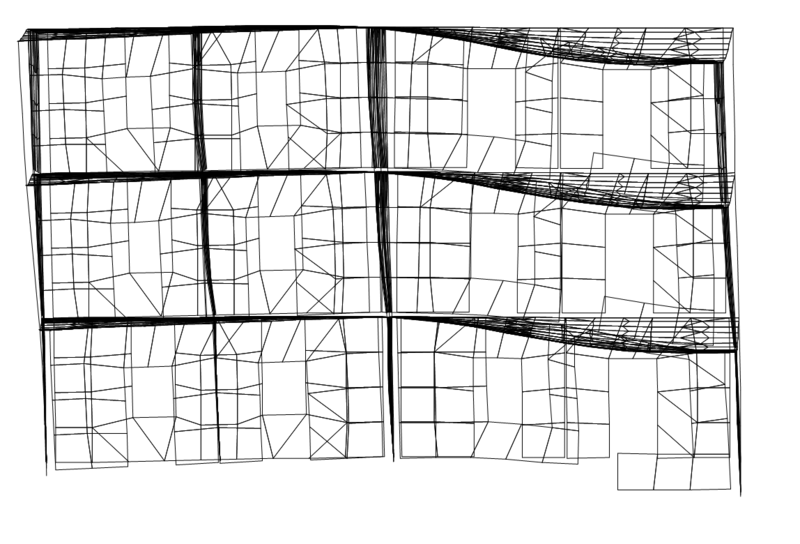
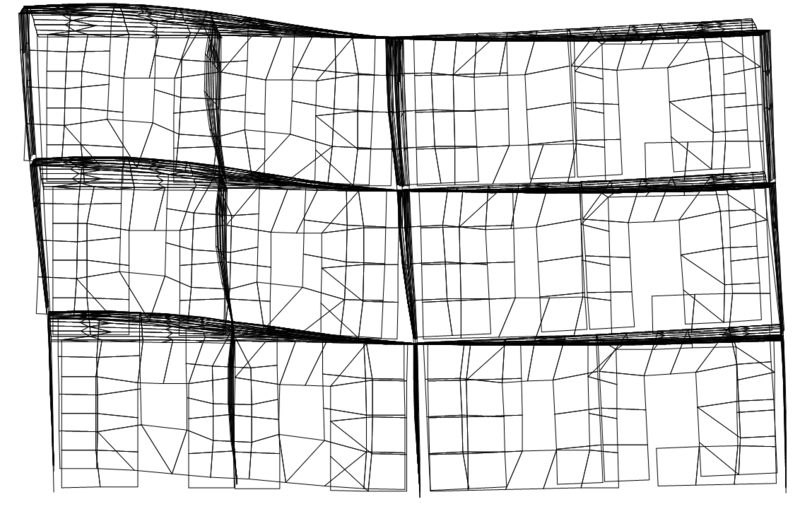
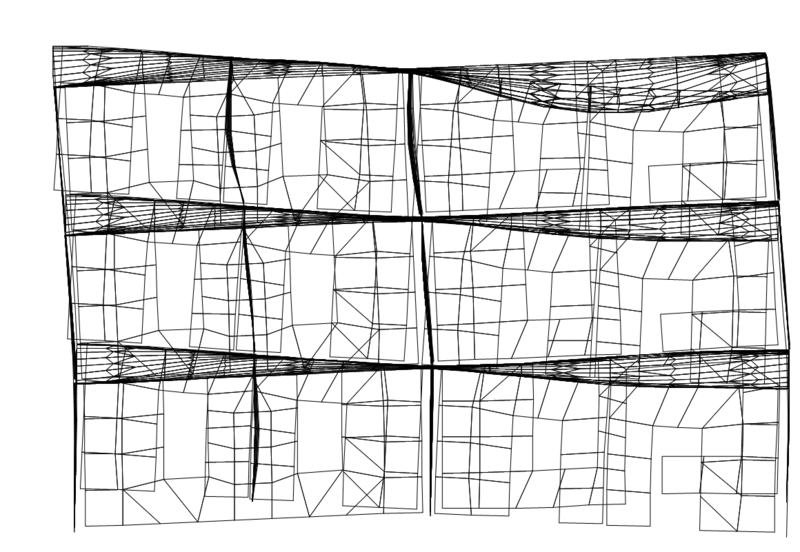
Первая и третья формы (поступательная и крутильная) колебаний КЭ-модели для конечного этапа испытаний при Т_рез. = 0,45 с представлены на рис. 3а и 3б. Высшие формы колебаний — четвертая, пятая и шестая — показаны соответственно на рис. 4а, 4б и 4в.

Рис. 4a. Высшие формы колебаний модели фрагмента. 4-я форма, вертикальные колебания колонн и диафрагм жесткости по оси 3, Т4=0,19 с Рис. 4б. Высшие формы колебаний модели фрагмента. 5-я форма, вертикальные колебания перекрытий и перегородок из плоскости, Т5=0,16 с Рис. 4в. Высшие формы колебаний модели фрагмента. 6-я форма, вертикальные колебания перекрытий, Т6=0,11 с

Быстродействие ВК SCAD Office (время решения задачи составило немногим более одной минуты) позволило проанализировать большое количество вариантов сочетания жесткостей специальных конечных элементов КЭ № 55 и КЭ № 51 и добиться максимального соответствия параметров КЭ-модели с экспериментальными данными.

Анализ КЭ-модели и ее сравнение с экспериментом

Основной вклад (69%) в сумму модальных масс обеспечивается за счет поступательных колебаний модели по первой форме. Влияние крутильной формы колебаний фрагмента незначительно и не превышает 1%. Согласно Eurocode-8 (версия 1995) [7] при динамическом анализе рекомендуется учитывать количество форм колебаний, обеспечивающее сумму модальных масс, не менее 90%. Первые пять форм колебаний фрагмента дали результат 98%. Таким образом, можно полагать, что динамические свойства модели обусловлены колебаниями системы по первым пяти формам.

Как уже сказано, подбор жесткостных параметров модели фрагмента производился с учетом только первой формы собственных колебаний, в силу чего одной из основных задач анализа является контроль за соответствием собственных частот КЭ-модели экспериментальным значениям на всем частотном диапазоне. С учетом результатов модального анализа этот диапазон собственных частот (с некоторым запасом) может быть обозначен как 2,2 ÷ 9,1 Гц. Такими «контрольными» значениями на указанном частотном диапазоне служат частоты (таблица 3):

• крутильных колебаний (3-я форма);
• колебаний перегородок из плоскости (5-я форма);
• вертикальных колебаний перекрытий (6-я форма).

Расхождения между расчетными параметрами модели и экспериментальными данными обусловлены двумя основными причинами:

• погрешностями принятой методики моделирования;
• особенностями практической реализации резонансного метода испытаний сооружений.

Таблица 3. Сравнение КЭ-модели с экспериментальными данными

Периоды колебаний, с/ Частоты, Гц	Формы колебаний
	1-я поступательные колебания	3-я крутильные колебания	4-я вертикальные колебания колонн и диафрагм жесткости по оси 3	5-я вертикальные колебания перекрытий, колебания перегородок из плоскости	6-я вертикальные колебания покрытия фрагмента
КЭ-модели	0,45 ⁄ 2,2	0,25 ⁄ 4,0	0,19 ⁄ 5,3	0,16 ⁄ 6,2	0,11 ⁄ 9,1
Экспериментальные	0,45 ⁄ 2,2	0,30 ⁄ 3,3	-	0,22 ⁄ 4,5	0,12 — 0,14 ⁄ 8,3 — 7,1

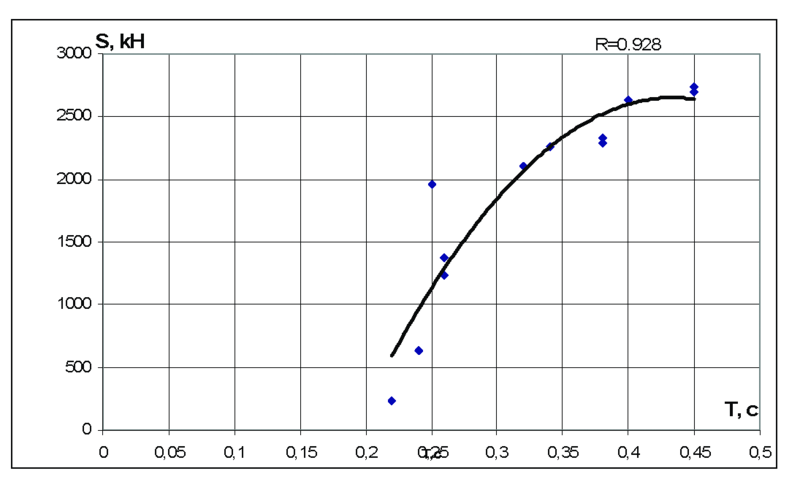
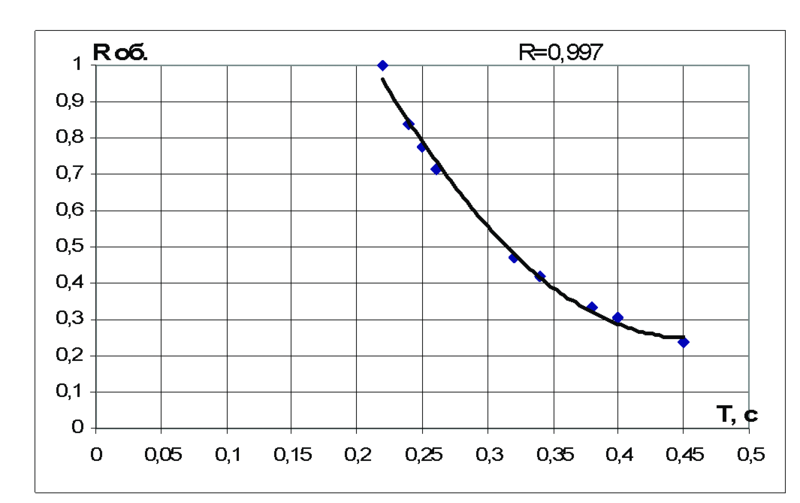
Графики зависимости от периода резонансных колебаний суммарной инерционной силы и снижения обобщенной жесткости фрагмента представлены на рис. 5а и 5б.

Рис. 5а. График зависимости от периода резонансных колебаний фрагмента инерционной нагрузки в кН Рис. 5б. График зависимости от периода резонансных колебаний фрагмента обобщенной жесткости фрагмента в %

Выводы

В статье изложен приближенный способ построения КЭ-модели фрагмента безригельного каркаса по результатам его вибрационных испытаний с высоким уровнем динамического нагружения, соизмеримого по интенсивности инерционной нагрузки с реальными сейсмическими воздействиями. Нелинейная нестационарная модель фрагмента представлена в виде последовательности линейно-упругих одномассовых систем, частоты которых соответствуют частотам резонансных колебаний на различных этапах вибрационных испытаний фрагмента. При построении расчетной модели использован ВК SCAD Office. Регулирование обобщенной жесткости фрагмента за счет изменения жесткостей специальных конечных элементов позволило добиться максимального совпадения параметров КЭ-модели с экспериментальными данными. Указанная модель может найти применение при расчетах зданий на сейсмические воздействия с использованием прямого динамического расчета. При этом в качестве внешнего воздействия применяется стандартный набор расчетных моделей сейсмических движений основания в функции времени.

Литература

1. Поляков С.В., Килимник Л.Ш., Жунусов Т.Ж., Ицков И.Е., Никипорец Г.Л. Методика анализа результатов вибрационных испытаний зданий и крупномасштабных панелей // Строительная механика и расчет сооружений, 1986, № 2, с. 52−56.
2. Бержинская Л.П. Автореферат диссертации на соискание ученой степени кандидата технических наук «Надежность региональных типов зданий при сейсмических воздействиях (на примере Прибайкалья)» // Улан-Удэ, 2006. 22 с.
3. Ден-Гартог Дж. П. Механические колебания (перевод с 4-го американского издания). — М.: Физматгиз, 1960. 580 с.
4. SCAD OFFICE. Вычислительный комплекс SCAD. — М.: Изд-во Ассоциации строительных вузов, 2004. 590 с.
5. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа. — Киев: Сталь, 2002. 596 с.
6. Инструкция по проектированию конструкций панельных жилых зданий ВСН 32−77. — М.: Стройиздат, 1978, с. 109−111.
7. Eurocode-8 (version 1995): Earthquake Resistant Design of Structures// Brussels: European Committee Standardization, 1995. 56 p.