Главная » CADmaster №2(32) 2006 » Машиностроение
Опыт использования программного комплекса MSC.AFEA в КБ Точмаш имени А.Э. Нудельмана
В одном из предыдущих номеров журнала авторы этих строк, представляя результаты тестирования программного комплекса MSC.AFEA, обещали поделиться опытом его использования для решения более сложной задачи. Пришло время выполнить обещание, тем более что MSC.AFEA успел зарекомендовать себя в КБТочмаш с самой лучшей стороны…
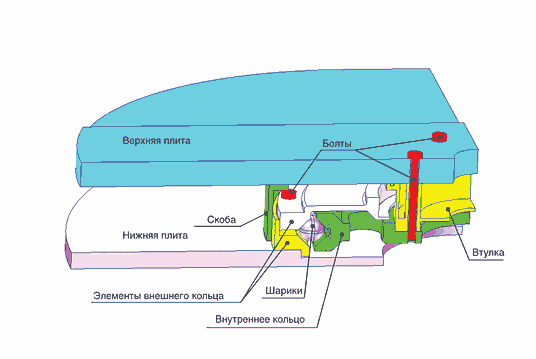
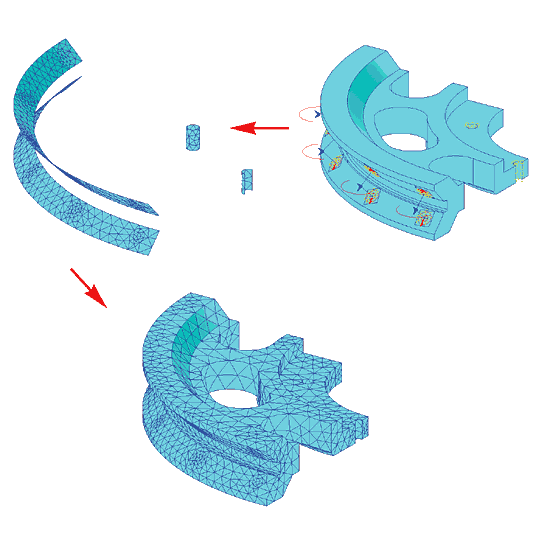
Повторим постановку задачи. Рассматривается поведение подшипника, который в процессе эксплуатации нагревается на 60 °C и нагружается осевой силой в три тонны. В качестве расчетной области рассматривается ¼ часть подшипника (рис. 1), выделенная по признаку симметрии (геометрической и по нагрузке).
В состав подшипника входят компоненты, изготовленные из разных материалов. Сваренные между собой верхняя плита и скоба выполнены из алюминиевого сплава, нижняя плита — из титана, а остальные компоненты — из стали. Особенность задачи заключена в предварительной затяжке деталей подшипника таким образом, что напряжение в сечении болтов составляет 50 кгС/мм2.
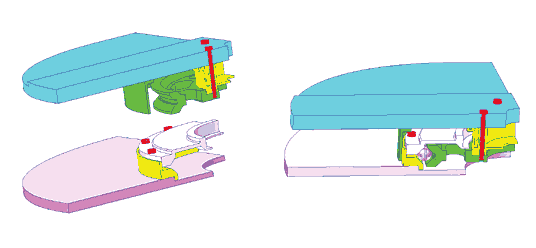
На рис. 2 показаны части подшипника, скрепленные болтами, взаимодействие между которыми передается только через шарики. Соответственно болты вкручиваются во внутреннее кольцо подшипника и в нижнюю плиту (соответственно верхняя и нижняя часть сборки).
Основной вопрос мы сформулировали так: «Не произойдет ли вследствие разного температурного расширения разнородных материалов заклинивание шариков при нагреве подшипника?»
Большое количество контактных поверхностей делает задачу существенно нелинейной и, с точки зрения инженерного анализа, действительно непростой. В то же время при всех ее сложностях хотелось «честно», без упрощений, смоделировать поведение конструкции, максимально учесть все нюансы.
Прежде всего предстояло определиться с моделированием предварительной затяжки болтов. Нередко ее моделируют, задавая соответствующее изменение температуры крепежных элементов по сравнению с начальной. Этот способ наименее трудоемок, но в данном случае его использование было бы некорректным: болты вкручиваются в один из компонентов подшипника (это моделируется как условие склейки (Glue) соответствующих поверхностей) и искусственное изменение их температуры вызвало бы появление напряжений в точках склейки, которых в реальной конструкции нет. В итоге был выбран другой вариант. По элементарной формуле сопромата предварительно рассчитывалась осевая деформация цилиндрической части болта при закрепленных торцах, вызывающая в поперечном сечении напряжение в 50 кгС/мм2, а затем в расчетной схеме задавалось условие соответствующего относительного смещения двух берегов разреза цилиндрической части болта, вызывающее такую деформацию.
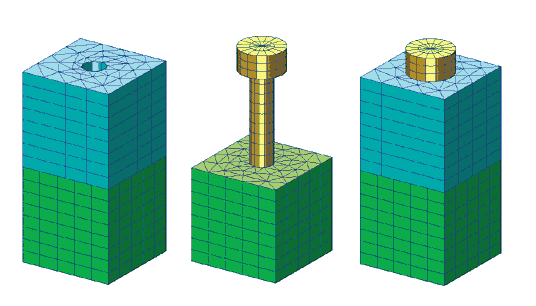
Проверка и отработка этого приема проводились на небольшой тестовой задаче. Два кубика с соосными отверстиями соединяются болтом (рис. 3). Болт вкручивается в нижний кубик, а его головка прижимает верхний кубик к нижнему.
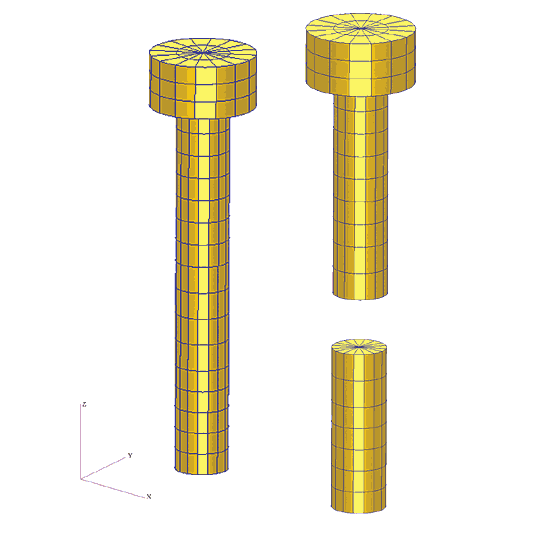
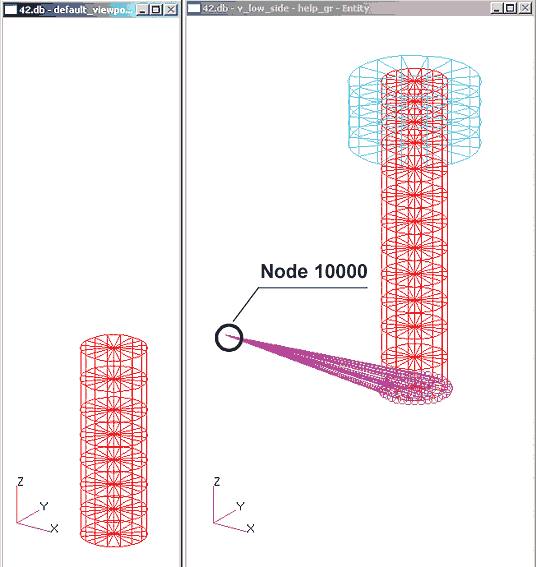
Для моделирования предварительной затяжки конечно-элементная модель болта разрезается на две части (в цилиндрической части по плоскости стыка конечных элементов), при этом узлы в месте стыка дублируются (рис. 4).
Таким образом, болт представляет теперь два набора конечных элементов, не связанных между собой. На месте стыка вводятся MPC 1, то есть уравнения связи между степенями свободы узлов, лежащих в плоскости разреза, в виде линейного полинома первой степени.
Чтобы обеспечить заданную предварительную затяжку, необходимо связать перемещения узлов по осям X и Y глобальной системы координат, а по оси Z (вдоль этой оси направлена ось болта) ввести следующее условие:
Uzn (перемещение по оси Z узла, принадлежащего нижнему берегу разреза) = Uzv (перемещение по оси Z узла, принадлежащего верхнему берегу разреза) + Delta Uz (перекрытие двух берегов разреза, обеспечивающее преднатяг).
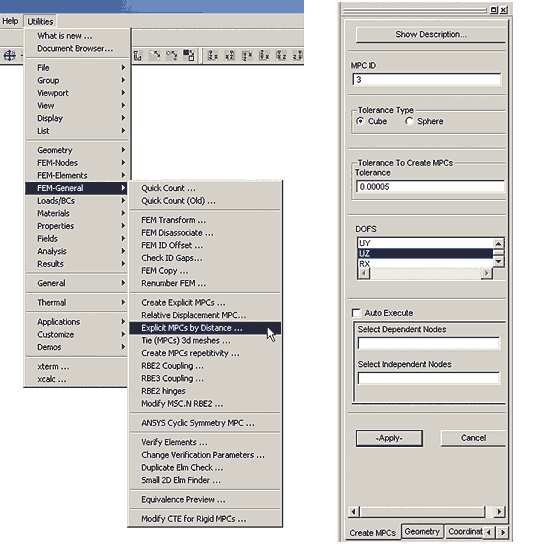
Для задания ограничений проще всего воспользоваться утилитой Explicit MPCs by Distance, которая позволяет вводить связи между двумя совокупностями узлов, связывая близлежащие пары (рис. 5). При этом пары связываются, если они расположены на расстоянии, не превышающем задаваемого допуска (Tolerance to create MPC).
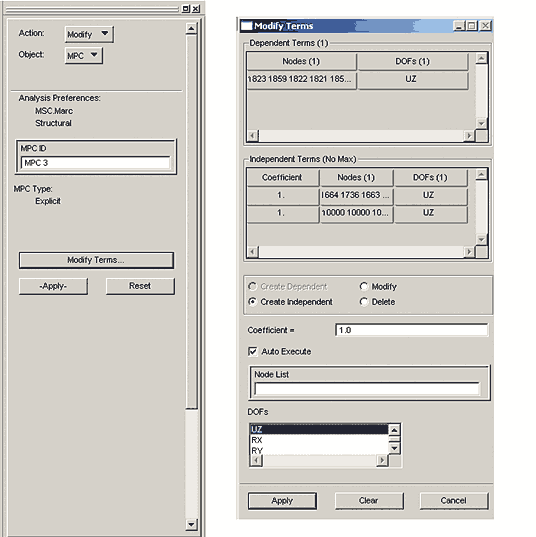
Последовательно выполняя эту команду для перемещений UX, UY и UZ, получаем три ограничения MPC. Если для перемещений по осям Х и Y MPC сформированы в окончательной форме как UXn=UXv, UYn=UYv для каждой пары узлов, то MPC, соответствующее перемещениям по оси Z, надо подкорректировать. Для этого в пространстве определяется узел (в данном случае с глобальным номером 10000), на который накладывается условие предписанного перемещения (UX=0, UY=0, UZ=Delta UZ), а затем активируется команда редактирования ограничений Elements/Modify/MPC (рис. 6).
Далее вводится корректируемый номер MPC — в нашем случае это MPC3.
При нажатии кнопки Modify Terms… появляется дополнительное окно c одноименным заголовком. В поле Node List этого окна многократно дублируется номер ссылочного узла (по количеству узлов в сечении). На рис. 6 таблица Independent Terms показана уже после редактирования ограничения MP3. Закрываем окна (для этого требуется нажать кнопку Apply) и получаем требуемый результат: подкорректированный MPC3 соответствует ограничению UZn=UZv+DeltaUZ для всех пар узлов в сечении. Это ограничение отражается на расчетной схеме соответствующими графическими символами (рис. 7).
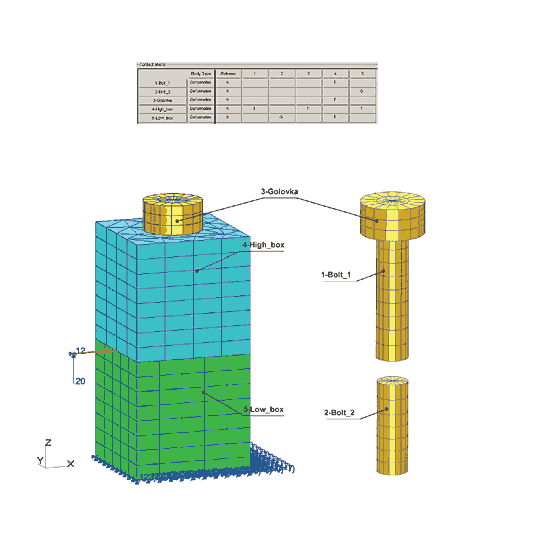
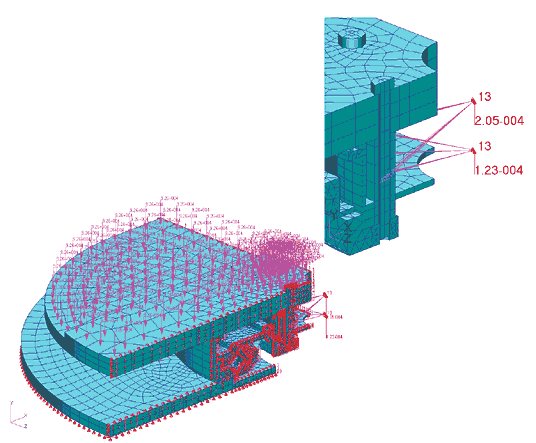
На сборку накладываются ограничения: нижний торец кубика (в который вкручивается болт) фиксируется, то есть перемещения узлов по всем направлениям задаются нулевыми (рис. 8). Здесь же приводится таблица, определяющая контактное взаимодействие между компонентами сборки.
Результаты расчета показаны на рис. 9.
Как видно из рисунка, решение выглядит вполне правдоподобным, в сечении свободной части болта напряжение близко к однородному и равно приблизительно 500 Н/мм2 (50 кгС/мм2), к чему мы и стремились.
После этого решено было приступить к решению основной задачи.
Сборка, выполненная в системе SOLIDWORKS, представляет собой совокупность 20 твердотельных объектов, включая пять болтов, три шайбы и пять шариков.
Практически во всех случаях, когда для решения задачи используется конечно-элементный комплекс, одним из важнейших и самых трудоемких шагов является построение рациональной конечно-элементной сетки, которая, с одной стороны, была бы достаточно подробной, чтобы адекватно представлять модель и обеспечивать приемлемые по точности результаты, а с другой — не приводила бы к чрезмерно большой размерности системы уравнений, что в свою очередь приводит к увеличению времени счета задачи.
В нашем случае расчетчики располагали машиной Pentium IV с тактовой частотой процессора 1700 Мгц и оперативной памятью 2 Гб.
Для представления трехмерных областей в MSC.Patran используется несколько типов конечных элементов: гексаэдры (шестигранные «кирпичи»), пятигранные призмы и тетраэдры. С точки зрения точности получаемых результатов и простоты оценки качества сетки предпочтение следует по возможности отдавать гексаэдрам. При меньшем их количестве в модели (по сравнению с тетраэдральными элементами) вполне реально получить более точные результаты. Впрочем, такими элементами можно представить не любую деталь, тогда как тетраэдральные элементы в этом смысле более универсальны.
Мы применили в модели все три вида конечных элементов, причем для более точной аппроксимации криволинейных границ использовались изопараметрические элементы второго порядка с квадратичными функциями формы.
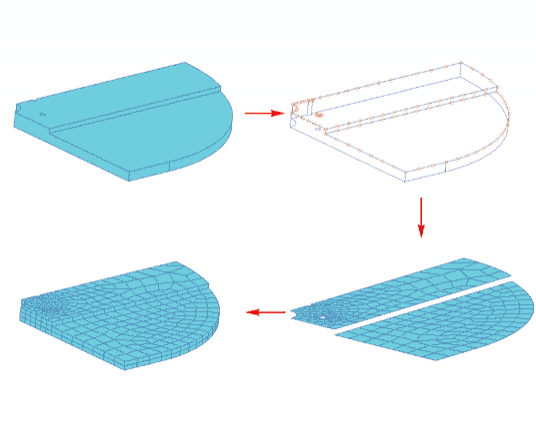
Последовательность действий при формировании сетки для верхней плиты подшипника представлена на рис. 10.
Первоначально была создана плоская сетка на двух поверхностях. Параметры сетки регулировались путем задания так называемых «точек разметки КЭ-сетки» (Mesh Seeds), которые определяют положение точек на кривых, и заданием среднего размера конечного элемента. Затем методом выдавливания вдоль глобальной оси Y получены трехмерные элементы (гексаэдры и призмы). Таким же образом формировались конечно-элементные модели нижней плиты, болтов, скобы и шайб (рис. 11).
Следует отметить, что в отличие от других элементов подшипника трехмерная сетка скобы формировалась иначе — путем вращения плоского образца вокруг вертикальной оси (команда Sweep/Element/Arc).
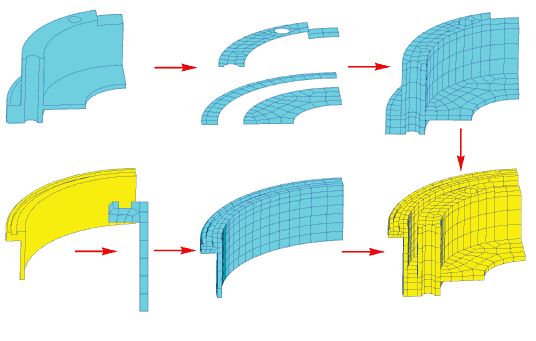
Несколько более трудоемким оказался процесс создания сетки для втулки (рис. 12). Этот компонент был разделен средствами MSC.Patran на две части. Дискретизация одной из них выполнялась путем выдавливания предварительно построенных сеток вдоль глобальной оси Y (как и в предыдущих случаях), а трехмерная сетка для второй получена путем вращения сечения (с заранее построенной конечно-элементной сеткой) вокруг оси Y. Конечно, при этом необходимо заранее предусмотреть, чтобы сетки с определенной точностью совпадали по сопрягаемым поверхностям. После этого выполняется операция слияния совпадающих узлов по этим поверхностям.
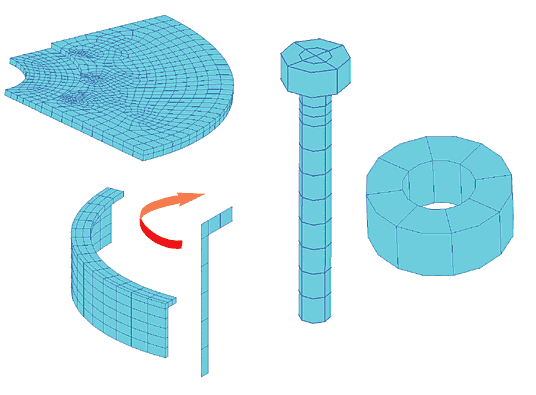
Остальные тела, в том числе и шарики, были разбиты на 10-узловые тетраэдры. На поверхностях, с которыми контактируют шарики, предварительно строились двумерные сетки (Elements/Create/Mesh/Surface/Paver) со сгущением в местах предполагаемого контакта. Рис. 13 иллюстрирует эту технологию на примере конечно-элементной разбивки внутреннего кольца подшипника.
Для сгущения сетки строились дополнительные кривые (окружности), лежащие в плоскостях, касательных к поверхности контакта. Затем они проецировались на криволинейные поверхности, а после ассоциации проекций кривых с этими поверхностями назначались Mesh Seeds и выполнялось построение сетки на поверхности. Следующим шагом осуществлялась генерация тетраэдров (Elements/Create/Mesh/Solid/TetMesh). При этом расположение узлов на предварительно разбитых поверхностях сохраняется.
По завершении построения конечно-элементной сетки были сформированы краевые условия, к числу которых также относится информация по контактным областям.
Контактные области (а каждой из них присваивается собственное уникальное имя) можно формировать, непосредственно указывая геометрические объекты — в таком случае в качестве контактных областей выбираются конечные элементы, ассоциированные с этими фигурами. Кроме того, контактную область можно создавать, непосредственно задавая список конечных элементов.
Ассоциированные конечные элементы автоматически образуются при выполнении процедуры конечно-элементного разбиения геометрических объектов: объемных тел (солидов), поверхностей и кривых — Elements/Create/Mesh/Solid (Surface, Curve). Если получать конечные элементы на основе конечно-элементных сеток меньшей размерности путем экструзии, вращения
В рассматриваемой задаче такая ассоциация была введена для конечных элементов, представляющих верхнюю и нижнюю плиты, а также втулку и скобу. При задании краевых условий в виде предписанных перемещений это позволило ссылаться на соответствующие поверхности «солидо» (в противном случае пришлось бы вводить список узлов, лежащих на этих поверхностях). На рис. 14 представлена расчетная область с маркерами краевых условий по перемещениям и нагрузкам. По плоскостям симметрии наложены ограничения на перемещение узлов в направлении, перпендикулярном этим плоскостям (эти перемещения равны нулю). Также запрещены перемещения в вертикальном направлении узлов на невидимой поверхности нижней плиты. Предварительная затяжка болтов смоделирована с использованием MPC по аналогии с тестовым примером.
Чтобы улучшить кинематическую определимость расчетной модели и вычислительную устойчивость решения в отдельных узлах шариков и верхней части подшипника, которая имеет возможность перемещаться в вертикальном направлении, введены нуль-мерные элементы типа SPRING (пружина) с невысокой жесткостью.
Для моделирования истории нагружения конструкции сформированы три группы нагрузок (LOAD CASE). Первая соответствует предварительному затягу болтов в конструкции, вторая — нагреву элементов подшипника на 60 °C, а третья — равномерной загрузке верхней плиты силой в три тонны.
Необходимо отметить, что в препостпроцессоре MSC.Patran опции просмотра, редактирования и удаления позволяют очень удобно манипулировать нагрузками и краевыми условиями. Также не составляет большого труда редактирование уже имеющихся LOAD CASE и создание новых на основе ранее сформированных нагрузок/краевых условий и LOAD CASE.
Характерной особенностью контактных задач, решаемых с помощью решателя MSC.Marc (а именно он используется в программном комплексе MSC.AFEA), является задание контактных таблиц, где устанавливается характер взаимодействия компонентов конструкции между собой — причем для каждой пары контактных тел можно задать индивидуальные параметры, наиболее точно соответствующие особенностям взаимодействия. Например, для пары можно менять коэффициент трения, влиять на процесс формирования уравнений связи, определяя, какое из тел проникающее, а какое — противодействующее проникновению. Если для отдельных компонентов вводятся условия склейки, можно, в частности, определить значение растягивающего усилия, при котором связь разрывается.
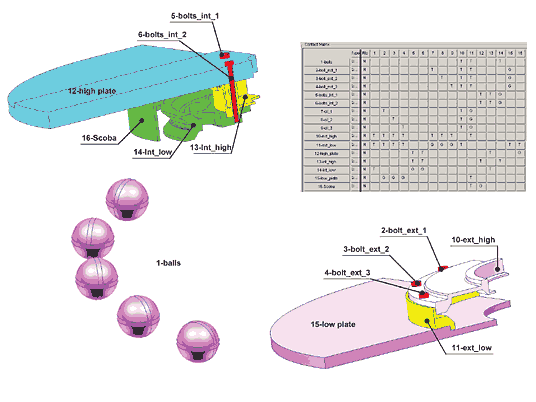
Таблица может модифицироваться при переходе от одного шага по нагрузке к другому. В нашем случае для всех LOAD CASE контактные таблицы идентичны (рис. 15), то есть набор контактных объектов и характер их взаимодействия при переходе от одной группы нагрузок к другой остаются неизменными.
Дадим некоторые пояснения к контактной таблице. Пять шариков объединены в одну группу (1-balls). Они могут вступать в контакт только с внутренним кольцом (14-int_low) и составным внешним кольцом (10-ext_high, 11-ext_low). Это отражено в таблице: напротив позиции 1-balls в колонках с номерами 14, 10 и 11 указан признак контактного взаимодействия (T — Touch, касание). Аналогично выражается отношение между остальными группами. Другой вариант контактного взаимодействия — склейка (G — Glue). В частности, это отношение установлено между внутренними болтами (5-bolts_int_1, 6-bolts_int_2) и внутренним кольцом (14-int_low). Позиции 7-cil_1, 8-cil_2, 9-cil_3 в таблице соответствуют шайбам, которые регулируют расстояние между двумя частями внешнего кольца подшипника.
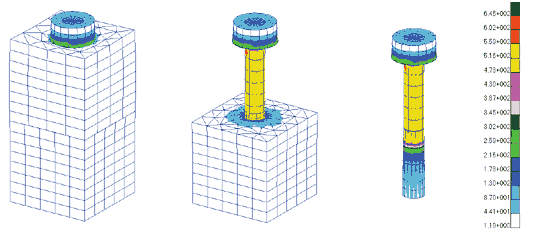
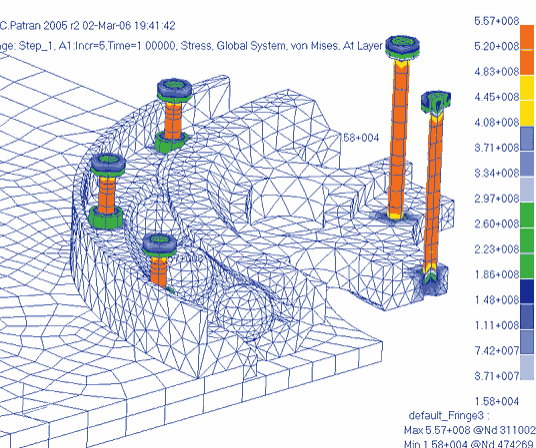
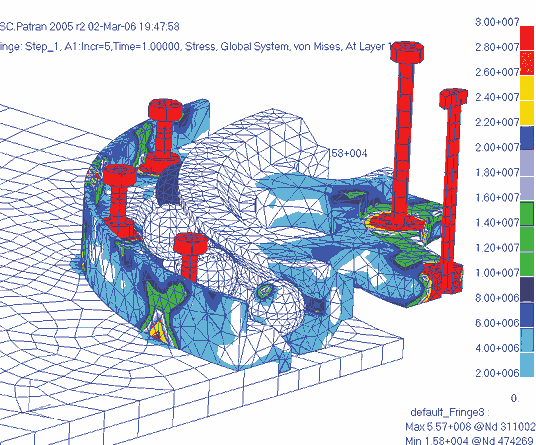
На рис. 16 показаны результаты расчета — эквивалентные напряжения по Мизесу — на момент окончания затяжки болтов (до уровня осевых напряжений, равных 50 кгС/мм2, размерность числовой шкалы — Н/м2).
Как видно из рисунка, наибольшие напряжения возникают непосредственно в болтах, а также в местах их контакта с другими компонентами сборки. В других частях конструкции напряжения оказываются ниже 3,7 кгС/мм2. Чтобы уточнить значения напряжений в менее нагруженных компонентах сборки, меняем диапазон шкалы (рис. 17).
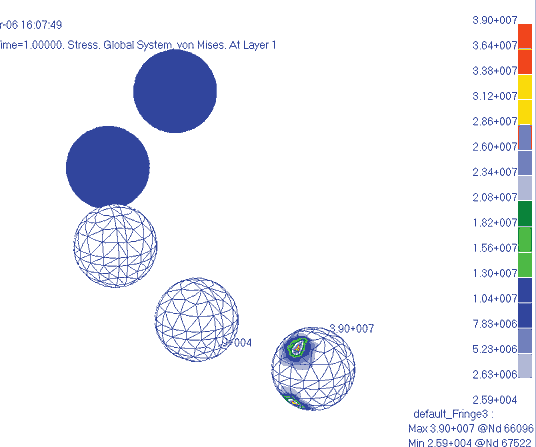
На рис. 18 показано поле эквивалентных напряжений в самих шариках на момент окончания затяжки болтов. Как видно, наибольшему сжатию подвергается крайний шарик, но контактные напряжения невелики (порядка 4 кгС/мм2).
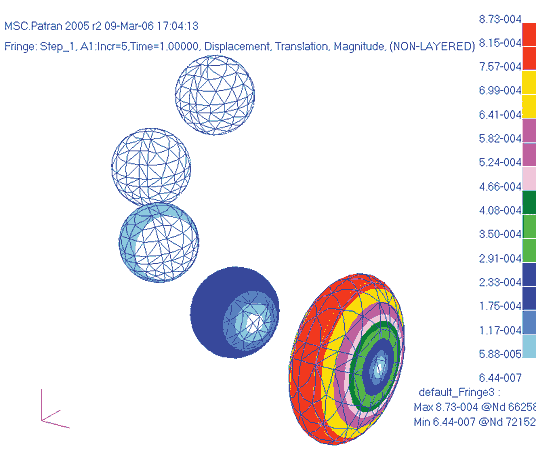
Перемещения (в значительно увеличенном масштабе) представлены на рис. 19.
Такая картина абсолютных перемещений свидетельствует, что в процессе взаимодействия шарик прокручивается вокруг своего геометрического центра. Максимальные перемещения составляют при этом порядка 1 мм.
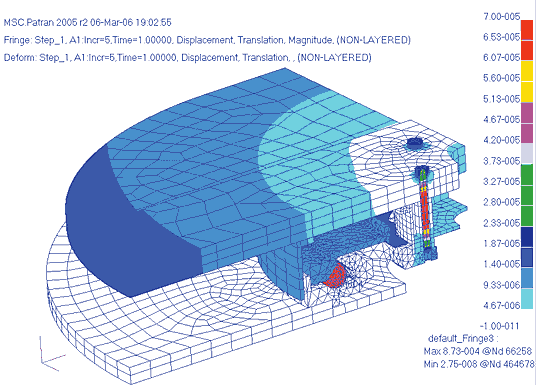
Общая деформационная картина показана на рис. 20.
На периферии верхней плиты наблюдаются большие перемещения, чем в центральной зоне, но по величине они незначительны — порядка сотых долей миллиметра, причем основной вклад вносят вертикальные составляющие вектора перемещений. Природа такого поведения конструкции объясняется деформациями в месте контакта болта с верхней плитой, вызывающими поворот плиты относительно горизонтальной оси, проходящей через головки болтов.
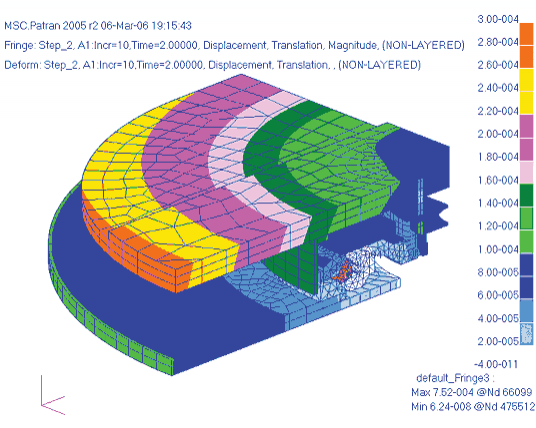
На рис. 21 показано распределение перемещений при нагреве конструкции на 60 °C.
Поле перемещений определяется в основном температурным расширением материалов конструкции. Коэффициент температурного расширения у алюминия примерно в 2,6 раза выше, чем у титана, поэтому примерно в той же пропорции отличаются и перемещения в точках верхней и нижней плит, равноудаленных от оси подшипника.
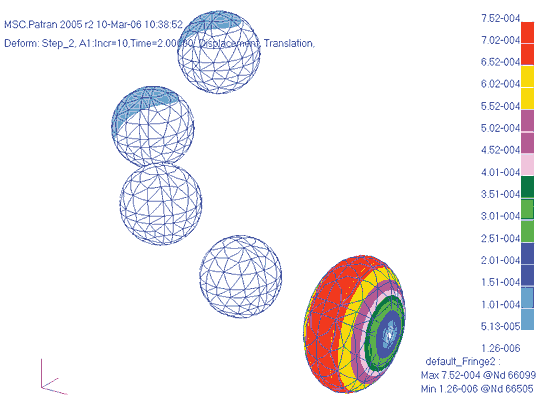
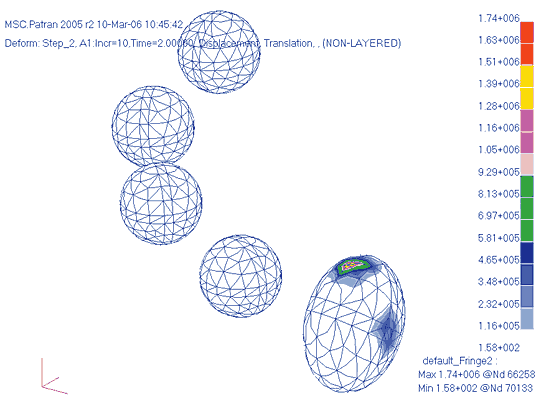
Что касается перемещений шариков, то максимальные значения соответствуют вращению вокруг центра тяжести шарика. Максимальные перемещения при этом также примерно равны 1 мм (рис. 22). Уровни напряжений в шариках после второй стадии нагружения не вызывают опасений (рис. 23). Максимальные напряжения по Мизесу — порядка 0,2 кгС/мм2.
Таким образом можно с уверенностью утверждать, что нагревание подшипника на 60 °C от исходного состояния не повлияет на его функциональность и заклинивания не произойдет.
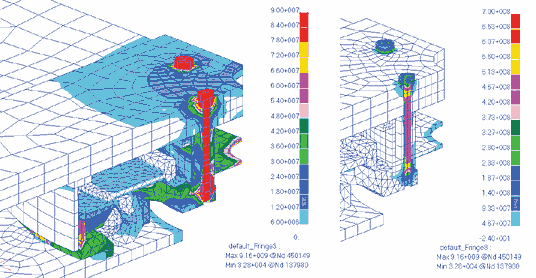
Нагружение подшипника равномерно распределенной силой в три тонны — третий этап расчета — также не вызывает опасных напряжений (рис. 24). Напряжения не превышают 7−9 кгС/мм2 в массивных элементах и 60 кгС/мм2 в болтах.
Таким образом, расчет подтвердил правильность конструкторского решения. В то же время следует отметить, что мощный функционал решателя MSC.Marc безусловно требует высокой квалификации пользователя. В нашем КБ еще только нарабатывается практика решения сложных задач с использованием решателя MSC. Marc — и результаты, приведенные в этой статье, были получены не сразу. Пришлось изрядно потрудиться над настройкой параметров решателя, поработать с разными вариантами расчетной модели, понадобились и консультации специалистов московского офиса MSC, за которые мы очень признательны. Но очередной этап преодолен, накоплен опыт, и мы с оптимизмом смотрим в будущее.
- Multipoint constrains. В буквальном переводе — многоточечные ограничения. ↑
начальник отдела
КБТочмаш
Сергей Моргулец,
начальник сектора
КБТочмаш
Максим Климов,
инженер КБТочмаш
Сергей Девятов,
ведущий специалист
компании CSoft
Тел.: (495) 069−4488
E-mail: devyatov@csoft.ru
Скачать статью в формате PDF — 526.7 Кбайт |