Главная » CADmaster №5(30) 2005 » Архитектура и строительство Применение многофронтального метода в программе SCAD для анализа большеразмерных расчетных моделей зданий и сооружений
Программа SCAD широко применяется для расчета пространственных конечно-элементных (МКЭ) моделей зданий и сооружений на статику, динамику и устойчивость. Такие расчеты связаны с проблемой решения систем линейных алгебраических уравнений с симметричной разреженной матрицей коэффициентов. Учитывая тенденцию неуклонного роста размерности задач (порядок систем МКЭ уравнений достигает 200 000−600 000 уравнений и более), а также тот факт, что при поиске приемлемого конструкторского решения приходится многократно вносить изменения в расчетную модель и, следовательно, каждый раз выполнять МКЭ-анализ заново, возникает потребность разработки и внедрения в расчетные программные комплексы высокоэффективных методов решения систем МКЭ-уравнений.
Рассматривается многофронтальный метод факторизации разреженных матриц, внедренный в программу SCAD версии 11.1. В отличие от версии 7.31, эта версия программы не содержит ограничений на количество узлов и конечных элементов расчетной модели, что предъявляет высокие требования к эффективности модуля решения системы уравнений (решателя) — снятие указанных ограничений приводит к значительному росту размерности решаемых задач. Способам повышения эффективности упомянутого многофронтального метода и посвящается эта статья.
Напомним, что факторизацией [1, 2, 3] называется процедура разложения K=LU заданной матрицы K в произведение верхней и нижней треугольных матриц L, U. Если матрица K — симметричная, то целесообразно применять разложение K=LDLT или K=LSLT, где L, D, S — нижняя треугольная матрица, диагональ факторизованной матрицы и диагональ знаков (то есть массив, состоящий из ±1).
Ответственными моментами при создании эффективного прямого метода решения систем МКЭ-уравнений являются упорядочение, рациональная работа с КЭШ-памятью и шиной, а также организация работы с данными.
Упорядочение состоит в перенумерации уравнений и обычно преследует две цели. Первая — уменьшить количество заполнений, возникающих при факторизации матрицы. Под заполнениями понимаются ненулевые элементы, возникающие в матрице при ее факторизации на позициях нулевых элементов исходной матрицы. Количество заполнений существенно зависит от того, в каком порядке расставить уравнения [2].
Другая цель — разделить данные на примерно равнозначные с точки зрения вычислительных затрат порции с целью эффективного распараллеливания операций в параллельных вычислительных системах. Поскольку эта статья ориентирована исключительно на пользователей персональных компьютеров, ограничимся рассмотрением только первого аспекта упорядочения.
Решение задачи оптимизации количества заполнений в точной постановке требует не меньших вычислительных усилий, чем решение данной МКЭ-задачи со случайным образом расставленными уравнениями (отсутствие упорядочения). Поэтому на практике применяют эвристические алгоритмы упорядочения. Начиная с 70-х годов и до середины 90-х в МКЭ-программах как правило применялись профильные методы решения систем линейных алгебраических уравнений с разреженными матрицами [2, 3]. При этом задачей упорядочения являлась минимизация ширины профиля. Чаще всего для этой цели применялся обратный алгоритм Катхилла-Макки (RCM [2, 3]), а позднее — более эффективный метод Слоана [9].
С середины 90-х годов в коммерческие МКЭ-программы интенсивно внедряются методы, тонко учитывающие разреженную структуру матрицы жесткости (sparse direct solvers). При этом чаще всего применяется упорядочение алгоритмом минимальной степени и методом вложенных сечений [2, 3, 11].
Алгоритм минимальной степени на каждом шаге факторизации в качестве ведущего выбирает то уравнение, которое содержит наименьшее количество ненулевых коэффициентов.
Метод вложенных сечений рассекает исходную конструкцию на две (или более) подконструкции, примерно равных по количеству узлов. Затем для каждой из подконструкций процедура вложенных бисекций повторяется снова
Оказалось, что для вытянутых в одном направлении конструкций лучшие результаты обычно дает алгоритм минимальной степени, а для конструкций, подобных кубу, — метод вложенных сечений [6]. Применение смешанного подхода, в котором сначала несколько шагов выполняется методом вложенных сечений, а внутри каждой подконструкции используется упорядочение алгоритмом минимальной степени, в сочетании с работой на огрубленном графе смежности позволило получить устойчивый по эффективности для широкого класса конструкций многоуровневый метод упорядочения [13, 14].
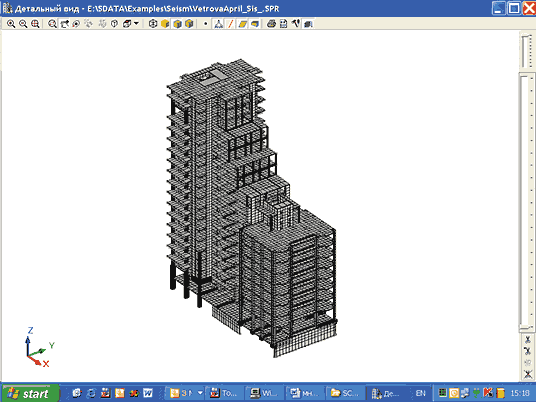
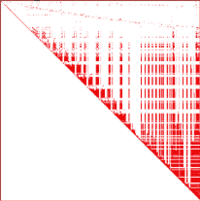
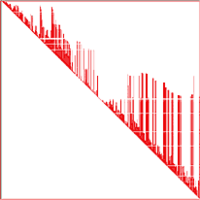
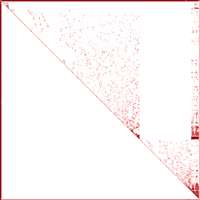
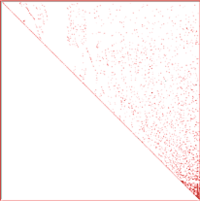
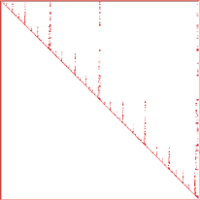
Таблица 1 иллюстрирует эффективность различных методов упорядочения для расчетной модели, представленной на рис. 1. Расчетная модель содержит 19 409 узлов, 19 456 элементов и 115 362 уравнения. В первой колонке приводятся ссылки на номер рисунка, изображающего расположение ненулевых элементов верхней треугольной матрицы при заданном методе упорядочения.
Таблица 1
| Номер рисунка | Тип упорядочения | Количество ненулевых элементов в факторизованной матрице, Мb | Объем матрицы, Мb |
|---|---|---|---|
| 2 | Отсутствие упорядочения | 490 366 701 | 3741 |
| 3 | Обратный алгоритм Катхилла-Макки RCM | 212 143 113 | 1618 |
| 4 | Алгоритм Слоана | 181 750 005 | 1386 |
| 5 | Метод параллельных сечений PSM | 45 281 385 | 345 |
| 6 | Метод вложенных сечений ND | 84 522 753 | 644 |
| 7 | Алгоритм минимальной степени QMD [2] | 27 501 777 | 209 |
| 7 | Алгоритм минимальной степени MMD [11] | 25 142 373 | 191 |
| 8 | Многоуровневое упорядочение [13, 14] | 25 341 381 | 193 |
Данный пример показывает, что при удачном выборе метода упорядочения объем перерабатываемой информации удается уменьшить на порядок и более (рис. 2−8).
Большое значение имеет способность алгоритма факторизации обеспечить высокопроизводительный режим вычислений, для оценки производительности которого обычно используется показатель q=ƒ/m (ƒ — количество арифметических операций,m — количество пересылок данных между оперативной памятью и кэшем процессора). Чем выше производительность алгоритма, тем больше значение q. Например, для алгоритма умножения вектора на вектор показатель эффективности равен 1/3 (учитываются только операции умножения, поскольку время выполнения одного умножения многократно превышает время выполнения операций сложения-вычитания). Для алгоритма умножения матрицы на вектор, для классического алгоритма исключения Гаусса в плотной матрице и для классического умножения матриц — q=1 (см. [1]). Если при этом две строки матрицы невозможно разместить в кэше, то указанные алгоритмы «скатываются» на уровень q=1/3. А это означает, что они обречены выполняться со скоростью медленной шины, осуществляющей пересылку данных «память — кэш -процессор», а не быстрого процессора. Совсем иначе дело обстоит с алгоритмом блочного умножения матриц. Если размеры блока таковы, что можно одновременно разместить в кэше три блока, то производительность алгоритма поднимается до уровня q ~ ![]() , где
, где ![]() — размер кэша [1]. Следовательно, для создания высокопроизводительной вычислительной системы надо избегать алгоритмов с уровнем производительности q ≤ 1 и стремиться так организовать вычислительный процесс, чтобы работать только с алгоритмами последнего типа (q ~
— размер кэша [1]. Следовательно, для создания высокопроизводительной вычислительной системы надо избегать алгоритмов с уровнем производительности q ≤ 1 и стремиться так организовать вычислительный процесс, чтобы работать только с алгоритмами последнего типа (q ~ ![]() ). Применительно к методу факторизации матрицы это означает переход от классической факторизации по строкам (по столбцам) к блочной факторизации, позволяющей удержать уровень производительности порядка q ~
). Применительно к методу факторизации матрицы это означает переход от классической факторизации по строкам (по столбцам) к блочной факторизации, позволяющей удержать уровень производительности порядка q ~ ![]() .
.
Высокая производительность метода решения системы МКЭ-уравнений будет обеспечена только тогда, когда эффективное упорядочение и высокопроизводительный режим работы с процессором сочетаются со способностью метода эффективно работать с данными, размещенными как в оперативной памяти, так и на диске. Прямые методы для разреженных матриц, использующие сжатый формат Шермана [2, 3], эффективно работают до тех пор, пока данные удается разместить в оперативной памяти компьютера. Поскольку виртуализовать эти методы весьма проблематично, их применение ограничивается относительно небольшими задачами.
Внимание исследователей привлекли многофронтальные методы [7, 8, 9], которые позволяют использовать эффективное упорядочение. Во фронтальном методе [12] сборка и исключение полностью собранных уравнений ведутся параллельно. Матрица жесткости системы в явном виде не собирается, а вместо этого добавляется поэлементно. Как только очередной узел оказывается собранным, ассоциированные с ним уравнения сразу исключаются. Говорят, что узел собран, если все элементы, примыкающие к этому узлу, уже включены в ансамбль, коэффициенты уравнений, связанные с этим узлом, полностью собраны и добавление последующих конечных элементов не будет вносить в них никаких изменений.
В результате факторизация производится в плотной матрице относительно небольшой размерности — фронтальной матрице, состоящей из полностью собранной части уравнений и не полностью собранной (так называемый незавершенный фронт). Полностью собранные уравнения сразу исключаются, а соответствующая часть матрицы записывается на диск. Далее добавляется очередной конечный элемент и снова исключаются собранные уравнения.
Если на расчетной модели выделить узлы, ассоциированные уравнения для которых образуют на данном шаге решения фронтальную матрицу, то эти узлы составят фронт. В процессе решения задачи фронт движется по узлам МКЭ-модели. Отметим, что при рациональном выборе очередности подачи конечных элементов на сборку можно добиться того, что размер фронтальной матрицы будет относительно небольшим. При решении задачи достаточно использовать алгоритмы и программы для плотных матриц.
Если в процессе факторизации одновременно образуется несколько фронтов, то метод называют многофронтальным. Такой подход оказывается эффективным как для параллельных вычислений, так и для обычных компьютеров.
Реализованный в программе SCAD многофронтальный метод [4, 5, 10] работает с любым упорядочением и является одной из возможных реализаций такого подхода. Первая версия этого метода, работающая только с двумя методами упорядочения (методом вложенных сечений и алгоритмом минимальной степени QMD [2]), имела два ограничения на размерность задачи. Первое обуславливалось тем, что фронтальная матрица максимального размера (максимальный фронт) должна поместиться в оперативной памяти компьютера. Это ограничение является принципиальным для фронтального (многофронтального) метода и сохраняется для всех последующих версий. «Продвинуться» в область задач большей размерности можно только двумя путями: нарастить оперативную память компьютера или использовать такое упорядочение, которое приводит к меньшей размерности максимального фронта. Второе ограничение связано с тем, что все незавершенные фронты хранились в виртуальной памяти адресного пространства процесса, что существенно ограничивало размерность решаемой задачи.
Эта версия была реализована в программе Robot Millennium (версия 5). Дальнейшее развитие метода шло в направлении разработки внутренней системы виртуализации хранения незавершенных фронтов (ранние релизы SCAD версии 7.31), улучшения методов и алгоритмов упорядочения (SCAD, осень 2004 года) и перехода к факторизации во фронтальной матрице, основанной на блочном LSLT -разложении, обеспечивающем высокопроизводительный режим (q ~ ![]() ), вместо постолбцового LU -разложения (q = 1/3) (SCAD, март 2005 года).
), вместо постолбцового LU -разложения (q = 1/3) (SCAD, март 2005 года).
Проиллюстрируем эффективность введенных усовершенствований на примерах двух больших задач.
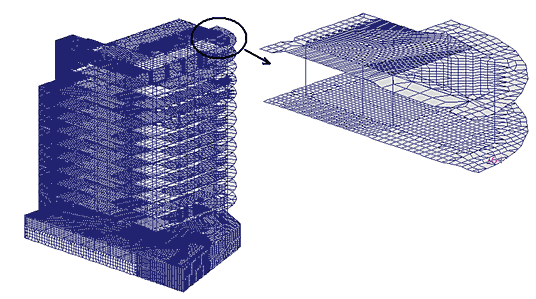
Пример 1. Рассматривается представленная на рис. 9 модель многоэтажного здания, содержащая 195 585 узлов и 204 067 элементов (1 171 104 уравнения).
Таблица 2 иллюстрирует возрастание производительности многофронтального метода [4, 5, 10] при улучшении качества упорядочения и переходе от классической факторизации во фронтальной матрице к блочной, обеспечивающей высокопроизводительный режим вычислений. В колонке 1 приведены данные для первых версий метода, реализованных в программах Robot Millennium и SCAD (версия 7.31, младшие релизы). В колонке 2 собраны результаты, полученные при использовании многоуровневого упорядочения (LU-факторизация), а в колонке 3 — при использовании как многоуровневого упорядочения, так и LSLT -факторизации во фронтальной матрице в блочном (высокопроизводительном) режиме.
Таблица 2
| Упорядочение/ метод факторизации | QMD [22]/LU | Многоуровневое/LU | Многоуровневое/LSLT | RCM/профильный метод |
|---|---|---|---|---|
| Столбец | 1 | 2 | 3 | 4 |
| Время решения | 5 ч 44 мин. | 3 ч 29 мин. | 1 ч 08 мин. | ~119 ч |
| Количество ненулей в матрице, Mb | 3246 | 2694 | 2694 | 21 606 |
Суммарный эффект — сокращение времени факторизации матрицы жесткости системы примерно в 5,5 раза по сравнению с первыми версиями метода. В четвертой колонке приведены результаты решения задачи традиционным профильным методом с упорядочением по обратному алгоритму Катхилла-Макки (RCM).
Исследования выполнены на компьютере средней производительности ПК Pentium-III (CPU 1266 MHz, RAM 1024 Mb).
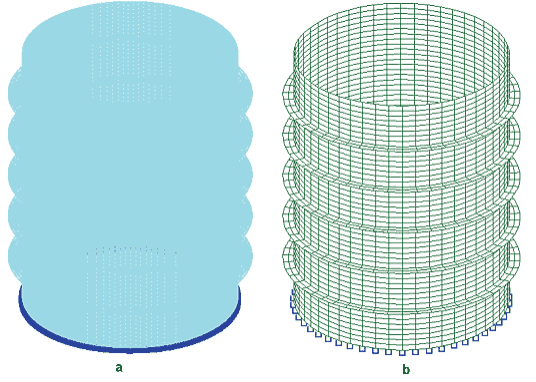
Пример 2. Рассматривается подкрепленная круговая тонкостенная цилиндрическая оболочка (рис. 10). МКЭ-модель включает 304 200 узлов и 300 300 элементов (1 819 800 уравнений). Поскольку исследуются особенности динамического поведения конструкции при сопряжении обшивки и ребер в дискретных точках, моделирующих точечную сварку, необходимо рассмотреть конечно-элементную модель с густой сеткой (левый рисунок). Поскольку на такой сетке трудно что-либо разобрать, то для удобства визуального восприятия на рисунке справа приведена модель с редкой сеткой. Результаты представлены в таблице 3.
Таблица 3
| Упорядочение/ метод факторизации | Метод вложенных сечений [2]/LU | Многоуровневое/LU | Многоуровневое/LSLT |
|---|---|---|---|
| Столбец | 1 | 2 | 3 |
| Время решения | 9 ч 51 мин. | 6 ч 40 мин. | 3 ч 46 мин. |
| Количество ненулей в матрице, Mb | 5216 | 4441 | 4441 |
Исследования выполнены на компьютере средней производительности ПК Pentium-III (CPU 1266 MHz, RAM 1024 Mb). Суммарный эффект — примерно трехкратное сокращение времени счета.
Описанный в статье блочный многофронтальный метод факторизации разреженных матриц прошел испытание большим количеством самых разнообразных задач, представленных многочисленными пользователями SCAD, и зарекомендовал себя как высокоэффективный и надежный решатель.
Литература
- Деммель Дж. Вычислительная линейная алгебра. Теория и приложения. М.: Мир, 2001. — 429 с.
- Джордж А., Лю Дж. Численное решение больших разреженных систем уравнений. М.: Мир, 1984. — 333 с.
- Писсанецки С. Технология разреженных матриц. М.: Мир, 1988. — 411 с.
- Фиалко С.Ю. К исследованию напряженно-деформированного состояния тонкостенных оболочек с массивными ребрами. // Прикл. механика, 2004. — Т. 40.
№ 4 , с. 84−92. - Фиалко
С.Ю. Сопоставление прямых и итерационных методов решения больших конечно-элементных задач строительной механики. — В кн.Перельмутер А.В. , СливкерВ.И. Расчетные модели сооружений и возможность их анализа. — Издание второе, — К.: Сталь, 2002. — с. 552−569. - Ashcraft C., Liu J. W.-H. Robust Ordering of Sparse Matrices Using Multisection. // Technical Report CS 96−01, Department of Computer Science, York University, Ontario, Canada, 1996.
- Duff I.S. Parallel implementation of multifrontal scheme. //Parallel Comput. — 1986. — 3 — P. 193−204.
- Duff I.S., Reid J.K. The multifrontal solution of indefinite sparse symmetric linear equations. //ACM Trans. Math. Software. — 1973. — 9 — P. 302−325.
- Duff I.S., Reid J.K., Scott J.A. The use of profile reduction algorithms with a frontal code. //Int. J. Numer. Meth. Eng. -1989 — 28 — P. 2555−2568.
- Fialko S.Yu., Kriksunov E.Z. and Karpilovskyy V.S. A sparse direct multi-frontal solver in SCAD software. Proceedings of the CMM-2003 — Computer Methods in Mechanics June 3−6, 2003, Gliwice, Poland. P. 131−132.
- George, A., Liu, J. W.-H., The Evolution of the Minimum Degree Ordering Algorithm, SIAM Rev. 31, 1−19 (March 1989).
- Irons B. A frontal solution of program for finite element analysis. //Int. J. Numer. Meth. Engrg. — 1970, — 2, P. 5−32.
- Karypis G., Kumar V., A Fast and High Quality Multilevel Scheme for Partitioning Irregular Graphs, Technical Report TR 95−035, Department of Computer Science, University of Minnesota, Minneapolis, 1995.
- Karypis G., Kumar V., METIS: Unstructured Graph Partitioning and Sparse Matrix Ordering System, Technical report, Department of Computer Science, University of Minnesota, Minneapolis, 1995.
Скачать статью в формате PDF — 244.0 Кбайт |