Главная » CADmaster №3(23) 2004 » Архитектура и строительство Поиск эффективных расчетных моделей ребристых железобетонных плит и перекрытий
В практике проектирования встречаются довольно сложные по конфигурации и форме монолитные конструкции и их элементы. При расчете таких конструкций актуальными оказываются вопросы их корректного моделирования в расчетной схеме [1] - с использованием средств, предоставляемых универсальными расчетными программами [2]. В частности, это касается моделирования таких, казалось бы, простых конструкций, как ребристые перекрытия, сборные ребристые плиты и плиты типа 2 Т, которые могут входить в состав того или иного сооружения или отдельной конструкции.
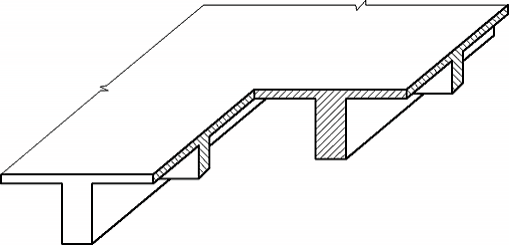
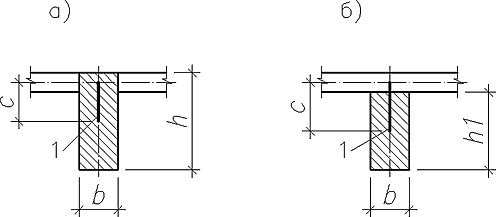
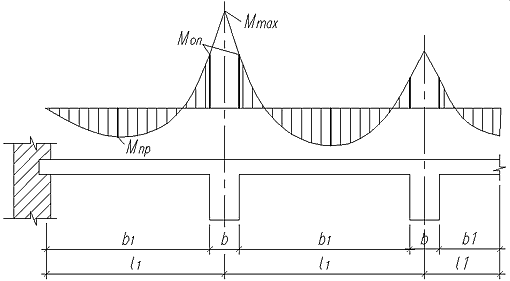
Ребристое перекрытие (рис. 1) состоит из плиты (балочной или опертой по контуру), второстепенных и главных балок. Все элементы перекрытия монолитно связаны между собой и представляют единое целое. Сущность конструкции монолитного ребристого перекрытия сводится к тому, что в целях экономии бетон изъят из растянутой зоны сечения. Сохранены лишь ребра, в которых сконцентрирована растянутая арматура и которые обеспечивают прочность элемента по наклонным сечениям.
Монолитное ребристое перекрытие конструктивно выполнено таким образом, что его верхняя поверхность является гладкой (балки не выступают из перекрытия). При расчете подобных конструкций с помощью современных вычислительных комплексов, которые базируются на методе конечных элементов (например, SCAD [2]), приходится оперировать такими общими моделями конструкций и их элементов, как стержень, плита, оболочка. Естественно, возникает вопрос, как разместить стержневой элемент по отношению к плитному: центрируя его по нейтральной линии плиты или смещая с определенным эксцентриситетом? Речь идет о том, как представить в расчетной схеме продольные и поперечные ребра и какая из расчетных схем будет наилучшим образом отражать действительную работу конструкции под действием нагрузки. По результатам расчетов какой из схем подобранная арматура будет наиболее рациональной?
Прежде всего необходимо заметить, что главный нормативный документ СНиП, касающийся железобетона [3], стыдливо умалчивает о существовании плит: указания по их расчету можно найти лишь в разнообразных рекомендациях и методиках [4], которым, наряду с достоинствами, присущи и определенные недостатки.
Автором этих строк проведен численный эксперимент, в котором было рассмотрено несколько расчетных схем с разным моделированием взаимного расположения ребра и плиты. При этом выполнено сравнение результатов расчета по выбранным схемам с результатами расчета по обычной для многих инженеров традиционной методике, которая приведена в пособии «Проектирование железобетонных конструкций» [5].
Для более полного понимания результатов эксперимента, их корректной трактовки и сравнения рассмотрим три ключевых момента, без уточнения которых невозможно в полной мере оценить полученные данные.
Определение напряженно-деформированного состояния плиты (перекрытия)
Метод конечных элементов, на котором базируется большинство современных вычислительных комплексов, относится к приближенным методам расчета. Тем не менее, сгущая сетку конечных элементов (путем последовательных приближений), можно приблизиться к точному решению. В этом случае при определении напряженно-деформированного состояния учитываются все силовые факторы, которые возникают в плите: изгибающие и крутящий моменты, поперечные силы.
В основе традиционного расчета по приближенной расчетной модели, которая базируется на методе предельного равновесия, лежит ряд упрощающих гипотез:
- плиту в состоянии предельного равновесия рассматривают как систему плоских звеньев, соединенных друг с другом по линии излома пластическими шарнирами, которые возникают в пролете по биссектрисам углов и на опорах вдоль балок;
- упругое защемление контура плиты (между балками) заменяют жестким;
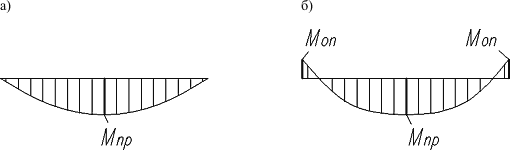
- жесткое соединение ребер (между собой) заменяют упругим. В частности, это касается расчетной схемы поперечного ребра при расчете сборной ребристой плиты перекрытия, которое представляет собою балку на двух шарнирных опорах. В действительности от заданной нагрузки в продольных ребрах возникает крутящий момент. Из условий равновесия узлов крутящий момент в продольном ребре будет изгибающим для поперечного — тогда действительная эпюра моментов будет иметь вид, представленный на рис. 2. Естественно, в случаях, когда соотношения габаритных размеров плиты больше четырех, величина опорного момента достаточно мала по сравнению с пролетным и им можно пренебречь. В то же время при меньших соотношениях (поскольку короткий стержень лучше оказывает сопротивление кручению) величина опорного момента в поперечном ребре становится сравнима с пролетным моментом и будет заметно влиять на величину усилия и, как следствие, на значение подобранной арматуры.
- нагрузки на ребра принимают по гипотетической схеме (в виде треугольников или трапеций).
Кроме того, необходимо указать на ограниченность класса задач, которые можно решить с помощью метода предельного равновесия (для плиты произвольного очертания неизвестна схема излома), принципиальную неприемлемость метода при комбинациях нагрузок, а также то, что указанный метод абсолютно ничего не говорит о трещиностойкости плит. Всё это касается плит, опертых по контуру, в которых соотношение сторон не превышает трех.
Для так называемых балочных плит (в которых l1/l2>3) суть расчета состоит в том, что на поле плиты вырезают полосы шириной 1 м вдоль короткой стороны, и расчетная схема плиты представляет собой многопролетную неразрезную балку. Поскольку плиту рассматривают между гранями балок, это позволяет уменьшить расчетные пролеты и, как следствие, пролетные моменты, опорные моменты и, соответственно, площадь подобранной арматуры.
При расчете как балочных плит, так и плит, которые оперты по контуру, крутящий момент во внимание не принимается.
Армирование плиты
Подбор арматуры в SCAD реализован на основе методики
Как уже сказано, расчет по традиционной методике не позволяет проконтролировать величину подобранной арматуры с учетом фактора трещиностойкости: сказываются ограничения самой методики и сделанные предположения.
Влияние схемы эксцентричного крепления ребра на результаты подбора арматуры в плите и ребре
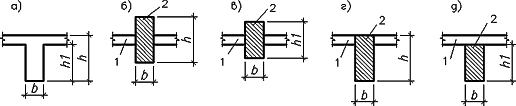
При моделировании поля железобетонной плиты пластинчатыми или оболочечными элементами и моделировании балок стержневыми элементами срединная плоскость пластин может быть расположена как на одном уровне, так и на разных уровнях с упругой частью стержня (рис. 3).
Можно было бы также представить ребра вертикально расположенными элементами плиты, однако в таком случае возникает вопрос о толковании размещения подобранной арматуры (рис. 4), поэтому в рамках этой статьи мы не будем рассматривать данный вариант.
При смещении стержневого элемента относительно нейтральной оси плиты возникает необходимость учесть эксцентриситет стыков элементов в узлах. Условия совместимости деформаций стержней и пластин будут выполнены при условии присоединения стержней к узлам пластин с помощью абсолютно жестких (EI = ∞) вертикальных вставок (рис. 5).
При этом в плите возникает мембранная группа усилий, которые в общем случае являются следствием корректного моделирования перекрытия. Следовательно, при эксцентричности стыков элементов в узлах плиты необходимо моделировать оболочечными элементами, которые имеют необходимое количество степеней свободы в узлах.
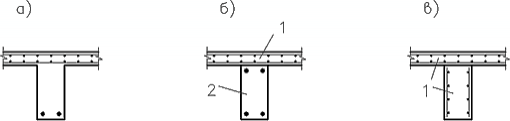
Если стержни примыкают к узлам пластин непосредственно (без жестких вставок), то в пластинах при вертикальной нагрузке мембранная группа усилий не возникает. Такое моделирование соответствует случаю, когда в реальной конструкции балки как бы выступают над плитами (рис. 6а, 6б). В этом случае при моделировании плиты конечными элементами плиты и оболочки результаты будут одинаковыми.
Каждый из предложенных на рис. 6 вариантов расчетных схем имеет свои преимущества и недостатки. В случаях, представленных на рис. 6а и 6б, жестких вставок нет. В случае, когда в стержневом элементе имеется вставка (рис. 6в, 6г), от действия вертикальной нагрузки в плите возникает мембранная группа усилий. Как следствие, в упомянутых стержнях появляется продольная сила (усилие распора), которая отвечает действительной работе конструкции. Этого не происходит при центрировании элементов по средней линии.
Кроме того, в схемах (рис. 6а, 6б и 6в) в местах пересечения стержня и плиты будет дважды учитываться площадь бетона. В схеме (рис. 6г) такого эффекта не наблюдается, но при этом возникает вопрос, правомерно ли будет перенести площадь подобранной арматуры в сжатой зоне стержня в сжатую зону плиты (изменение плеча внутренней пары сил).
Армирование стержневых элементов также возможно как по первой, так и по второй группам предельных состояний.
Рассмотрим два примера расчета (ребристой панели перекрытия и монолитного ребристого перекрытия с балочными плитами), которые приведены в пособии «Проектирование железобетонных конструкций», и по этим исходным данным смоделируем соответствующие расчетные схемы в комплексе SCAD (учитывая особенности, изложенные выше).
Ребра были представлены стержневыми элементами прямоугольного сечения. Тавровое сечение ребер не рассматривалось, поскольку, во-первых, при таком моделировании ребер будет дважды учитываться бетон сжатой зоны (стержня и плиты), что исказит конечный результат, а во-вторых, моделирование крайних ребер окажется некорректным, поскольку одна из полок тавра будет лишней.
Рассмотрено четыре типа схем, которые отличались между собой представлением нагрузки в расчетной схеме и типом конечного элемента плиты (табл. 1). Представление ребер одним типом элемента (пространственный стержень) при моделировании полки плиты конечными элементами оболочки и плиты объясняется тем, что стержневой элемент плоской схемы не может иметь жестких вставок в своей плоскости.
Таблица 1
| Тип схемы | Представление нагрузки в расчетной схеме | Тип элемента, которым моделируется | |
|---|---|---|---|
| полка плиты | ребро | ||
| 1 | Равномерно распределенная по всей поверхности плиты (с учетом собственного веса полки, ребер и временной нагрузки) [кН/м2] | Оболочка | Пространственный стержень |
| 2 | Плита | ||
| 3 | Равномерно распределенная по всей поверхности плиты (с учетом собственного веса полки, ребер и временной нагрузки) [кН/м2] + собственный вес ребер [кН/м2] | Оболочка | |
| 4 | Плита | ||
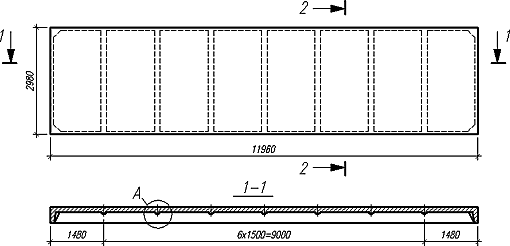
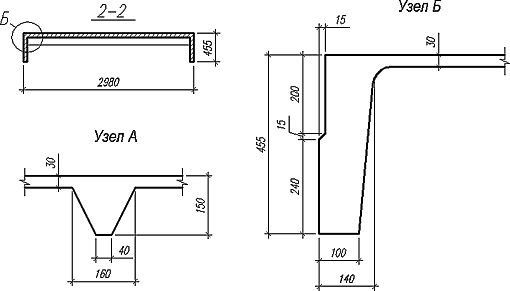
Пример 1. Рассмотрим железобетонную ребристую плиту перекрытия размерами 3×12 м. Плита состоит из контурных ребер высотой 450 мм, которые расположены по периметру плиты, и поперечных ребер, расстояние между которыми 1,5 м. Общий вид плиты и ребер показан на рис. 7. В расчетной схеме рёбра были приведены к эквивалентным по площади прямоугольникам. Полка плиты представляет собой однорядную многопролетную плиту, обрамленную ребрами.
При расчете, приведенном в пособии «Проектирование железобетонных конструкций», средние пролеты рассматривались как плиты, которые защемлены по контуру, а крайние — как плиты, защемленные по трем сторонам и свободно опертые на торцовые ребра (расчет выполняется методом предельного равновесия). Расчетные сечения продольных и поперечных ребер плиты были представлены в виде соответствующих тавров.
В SCAD, кроме комбинированной модели (стержень + плита или оболочка), был проведен и расчет стержневой модели, в которой продольные и поперечные ребра были представлены таврами с соответствующими расчетными размерами поперечного сечения. При этом рассматривалась загрузка поперечного ребра по двум схемам.
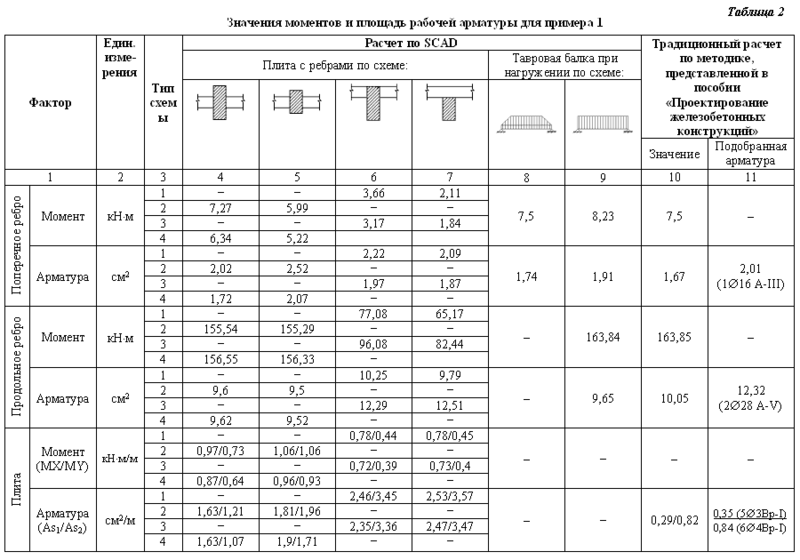
Результаты расчетов по разным схемам приведены в таблице 2. Здесь даны максимальные значения изгибающих моментов в пролетах ребер (взято среднее поперечное ребро). В последнем столбце показана подобранная арматура по результатам традиционного расчета. Как видно из результатов расчета для типов схем 1 и 3 с жесткими вставками, значения изгибающих моментов в ребрах значительно меньше, что можно объяснить действием мембранной группы усилий в оболочках. Результаты подбора арматуры отличаются не так сильно. Это объясняется тем, что при подборе арматуры в этих стержнях учитывалась продольная сила, которая является следствием возникновения распора в ребрах. Отличие результатов подбора арматуры между комбинированной и стержневой моделью можно объяснить тем, что для таврового сечения (при прочих равных исходных данных) требуется меньше арматуры, чем для прямоугольного — за счет большей площади сжатого бетона. В таблице для ребер приведены данные подбора арматуры при расчете с учетом трещинообразования.
Для плиты в таблице 2 приведены максимальные по полю плиты изгибающие моменты на единицу длины сечения (в числителе момент МХ, в знаменателе — MY).
Пример 2. Рассмотрим железобетонное монолитное ребристое перекрытие с балочными плитами, которое имеет размеры в плане 24×36 м (рис. 8). Главные балки размещены вдоль (по оси Х), а второстепенные — поперек (по оси Y).
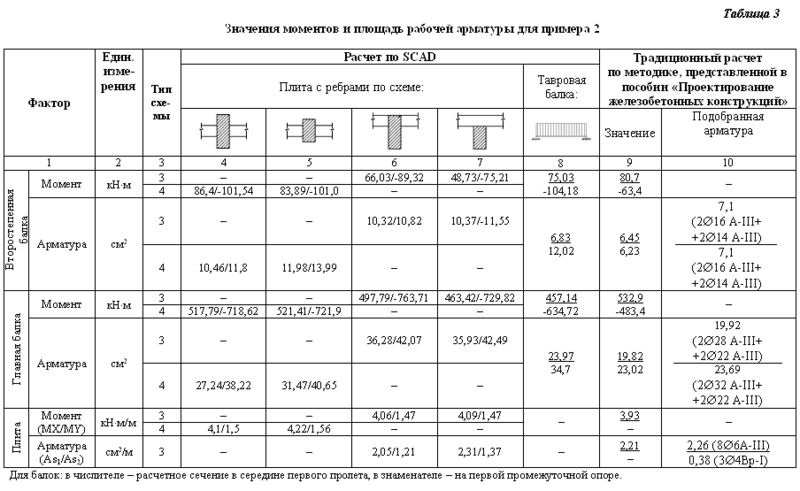
Результаты расчета и их сравнение для монолитного ребристого перекрытия приведены в таблице 3. Арматура для плиты подобрана по 1-й группе, для балок — по 1-й и 2-й группам предельных состояний. Поскольку расчетные схемы второстепенной и главной балок представляют собой многопролетные неразрезные конструкции, то для сравнения были выбраны сечения в первом крайнем пролете (значения в числителе) и на первой промежуточной опоре (значения в знаменателе). Знак «минус» указывает, что растянутое волокно находится сверху. Отличие в значениях изгибающих моментов объясняется тем, что при традиционном расчете расчетные пролеты для второстепенных балок принимают равными расстоянию между внутренними гранями главных балок (уменьшение пролета), а расчетные моменты на опоре берут по грани главных балок (уменьшение расчетного момента) (рис. 9). Как следствие, будет отличаться и величина подобранной арматуры. Такую же расчетную схему (с уменьшенными пролетами и моментами по грани балок) можно смоделировать и в конечно-элементной модели.
Отличие в усилиях, полученное по моделям, более ощутимо, чем различие в армировании плит, выполненном по полученным усилиям. Это объясняется следующими обстоятельствами:
- усилия в срединной плоскости плиты — сжимающие и воспринимаются бетоном практически без постановки дополнительной арматуры;
- в силу дискретности сортамента арматуры и применения стержней, как правило, только одного диаметра нивелируется различие между необходимой в разных случаях расчетной арматурой и той, которую реально использует производитель работ.
Анализ результатов расчета по предложенным моделям и сравнение их с результатами традиционного расчета дают право утверждать следующее:
- моделирование ребристого перекрытия или плиты стержневыми и плитными (оболочковыми) элементами по схемам, которые показаны на рис. 3, является корректным отображением реальной конструкции;
- результаты подбора арматуры в ребрах (балках) почти по всем предложенным моделям являются удовлетворительными;
- результаты подбора арматуры в полке плиты по сравниваемым методикам сходятся лучше, когда плита является балочной (работает в одном направлении);
- по результатам расчета и результатам подбора арматуры реальной конструкции наиболее точна схема моделирования ребристого перекрытия, в которой верхние грани ребра и плиты находятся на одном уровне (рис. 3г).
Литература
- А.В. Перельмутер,
В.И. Сливкер . Расчетные модели сооружений и возможность их анализа. — Киев, Сталь, 2002. — 600 с. - В.С. Карпиловский,
Э.З. Криксунов ,А.В. Перельмутер ,М.А. Перельмутер ,А.Н. Трофимчук . SCAD для пользователя. — Киев, ВВП «Компас», 2000. — 332с. - СНиП 2.03.01−84*. Бетонные и железобетонные конструкции / Госстрой СССР. — М., ЦИТП Госстроя СССР, 1989. — 88 с.
- Пособие по расчету статически неопределимых железобетонных конструкций. — М., Стройиздат, 1975. — 192 с.
- А.Б. Голышев,
В.Я. Бачинский ,В.П. Полищук и др. Проектирование железобетонных конструкций. — Киев, Будивельник, 1985. — 496 с. - Н.И. Карпенко. Теория деформирования железобетона с трещинами. — М., Стройиздат, 1976. — 204 с.
Киевский национальный университет
строительства и архитектуры,
ООО SCAD Soft (Киев)
Тел.: (10−38044) 243−7322
E-mail: scad@scadsoft.com
Скачать статью в формате PDF — 403.8 Кбайт |