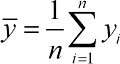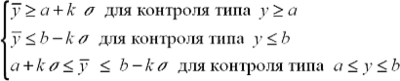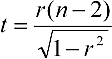CADmaster

Задача обеспечения качества приобретает сейчас все большее значение: в условиях конкурентной борьбы именно качество обеспечивает жизнеспособность предприятия. Само это понятие трактуется довольно широко: в него включают качество всех процессов, выполняемых на предприятии — начиная от целей, которые ставит перед собой руководство (качество цели), и заканчивая организацией конкретных производственных процессов (качество исполнения). Методической основой обеспечения качества являются стандарты международной организации по стандартизации ISO (International Standard Organization). Новейшая редакция этих стандартов в России — ГОСТ Р ИСО 9000−2001, ГОСТ Р ИСО 9001−2001 и ГОСТ Р ИСО 9004−2001. В соответствии с требованиями стандартов на предприятии должна быть создана система качества, регламентирующая выполнение всех действий согласно последним достижениям в области управления процессами. Система качества представляет собой совокупность задач, которые решаются на разных этапах производства, и методов (инструментов) их реализации. Основными являются методы математической статистики, что связано со статистической природой информации, порождаемой в производственных процессах. Действительно, даже при строгом соблюдении технологии на производственный процесс влияет множество случайных факторов, которые не позволяют получить желаемый детерминированный показатель качества. Это приводит к необходимости анализировать ситуацию в среднем, с вероятностной оценкой ожидаемого значения показателя.

Системы качества внедрены и успешно действуют на многих предприятиях, но теперь при заключении контракта потребитель хочет быть уверен не только в том, что у поставщика имеется такая система, но и в том, что она подкреплена соответствующими статистическими процедурами. В зависимости от уровня решения задач управления качеством устанавливается степень доверия к поставщику. При высшей степени доверия продукция может поставляться без приемочного контроля, что обеспечивает поставщику ощутимые экономические преимущества.

Учитывая всеобъемлющий характер вопросов управления качеством, можно предположить, что происходит формирование принципиально новой философии управления производством, в основе которой лежит критерий качества.

В статье, опубликованной в пятом номере журнала «CADmaster» за прошлый год ¹, рассмотрены вопросы реализации ряда статистических процедур управления качеством в системе TechnologiCS. Сегодня мы продолжим начатое обсуждение и приведем примеры применения процедур в производстве (большая часть примеров взята из ГОСТ) — с тем чтобы представить пользователям новые возможности управления качеством и перспективы развития статистических методов такого управления в системе TechnologiCS.

В левой колонке таблицы 1 приводятся пункты системы качества согласно стандартам ГОСТ Р ИСО 9001−2001, в правой — соответствующие статистические процедуры. Таблица составлена по материалам отчета ИСО/ТК 10  017 ². Исходными данными для работы процедур являются массивы информации, создаваемые по ходу управления производством в системе TechnologiCS. Задачи процедур и принципы их действия поясняются ниже.

Статистические процедуры обеспечения пунктов стандарта ГОСТ Р ИСО 9001−2001

Таблица 1

Анализ данных

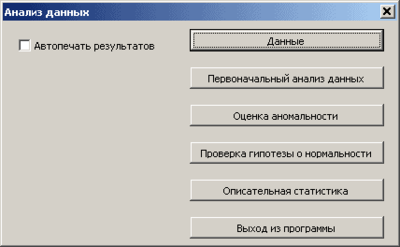
Цель этих процедур — первичный статистический анализ массива информации, порождаемого в результате измерения параметра, по которому производится управление. Основными результатами являются заключение о виде распределения параметра и точечные оценки характеристик генеральной совокупности, из которой получены измерения. Результаты имеют как самостоятельное значение, позволяя оценить степень соответствия статистических свойств реального процесса желаемым, так и вспомогательное, становясь основой для последующих процедур управления. На рис. 1 показана кнопочная форма программного модуля анализа данных.

Рис. 1. Кнопочная форма модуля анализа данных

Первой процедурой модуля является импорт массива данных и его структурирование в соответствии с определенными требованиями.

Далее следует процедура первоначального анализа, предусматривающая проверку массива данных на целостность и отсутствие синтаксических ошибок. Затем производится проверка гипотезы о наличии в исходных данных аномальных измерений (грубых ошибок). Эта задача решается в соответствии со стандартом СТ СЭВ 545−77, где рассмотрены различные условия наблюдения: при неизвестных генеральном среднем и дисперсии; в случае, когда известен один из этих параметров; при обоих известных параметрах.

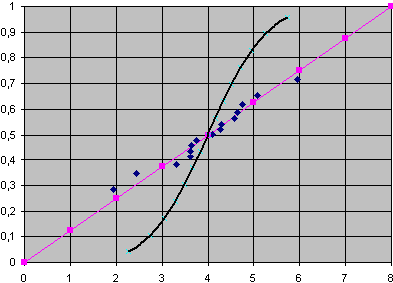
Следующая процедура — проверка гипотезы о нормальности распределения исходных данных по ГОСТ Р ИСО 5479−2002. В ходе реализации этой процедуры на этапе качественного анализа строятся экспериментальное и теоретическое интегральные распределения.

На рис. 2 сплошной кривой линией представлено интегральное стандартное нормальное распределение, сплошной прямой — то же распределение, отображенное путем специального преобразования в прямую линию. Ромбами на графике показаны значения, соответствующие анализируемым данным. Кучность, с которой эти значения группируются относительно прямой линии, показывает, что на качественном уровне распределение данных можно считать нормальным. Количественная проверка гипотезы о нормальности выполняется по таблицам ГОСТ.

Рис. 2. Нормальный вероятностный график

Заключительная процедура модуля — построение описательной статистики. Результатами являются среднее значение, дисперсия, медиана, мода, максимальное и минимальное значения массива исходных данных.

Оценки характеристик генеральной совокупности

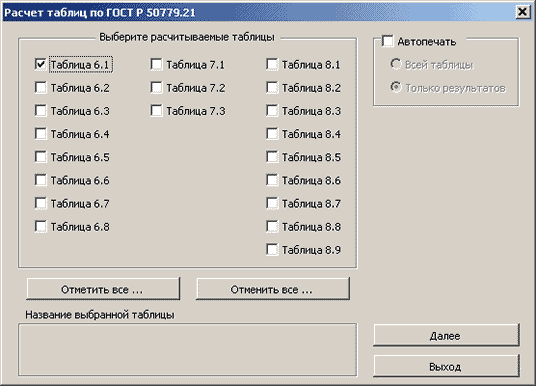
На рис. 3 показана кнопочная форма программного модуля оценки характеристик генеральной совокупности по ГОСТ Р 50  779.21−96 «Правила определения и методы расчета статистических характеристик по выборочным данным».

Рис. 3. Кнопочная форма расчета статистических характеристик по ГОСТ Р 50  779.21−96

В процедурах стандарта решаются следующие задачи:

• оценка среднего значения при известной дисперсии. Пример: определение центра настройки станка-автомата при условии, что его точность, определяемая разбросом получаемых размеров деталей без изменения настройки, считается известной;
• оценка среднего значения при неизвестной дисперсии. Пример тот же, что в предыдущем случае, но точность станка полагается неизвестной;
• сравнение среднего значения с заданным значением μ при известной дисперсии. Пример: проверка правильности настройки процесса на середину поля допуска при известной точности процесса;
• сравнение среднего значения с заданным значением μ при неизвестной дисперсии. Пример тот же, но дисперсия заранее неизвестна;
• сравнение двух средних значений при известных дисперсиях. Пример: технологический процесс обработки проводится одновременно на двух станках с известной точностью. Можно ли считать, что оба станка настроены одинаково?
• сравнение двух средних значений при неизвестных дисперсиях. Пример тот же, но точности неизвестны;
• оценка разности двух средних значений при известных дисперсиях. Пример: оценка разности средней толщины гальванического покрытия двух партий одинаковых изделий, изготовленных с одинаковой точностью;
• оценка разности двух средних значений при неизвестных, но равных дисперсиях. Пример тот же, но точности изготовления неизвестны;
• точечная или интервальная оценка дисперсии или стандартного отклонения. Пример: оценка точности показателя качества на выходе технологического процесса;
• сравнение дисперсии или стандартного отклонения с заданной величиной. Пример: оценка точности оборудования или технологического процесса в сравнении с известной точностью другого оборудования или процесса;
• сравнение дисперсий или стандартных отклонений двух генеральных совокупностей. Пример: сравнение точности двух станков-автоматов по результатам контроля геометрических размеров деталей;
• вычисление доли распределения случайной величины в заданном интервале (L, M) и вне его при известных параметрах нормального распределения. Пример: оценка ожидаемого уровня несоответствия показателя качества продукции при настройке станка на середину поля допуска или номинальное значение при известной точности;
• точечная оценка доли распределения случайной величины в заданном интервале (L, M) и вне его при известном стандартном отклонении или дисперсии. Пример: оценка уровня несоответствия показателя качества продукции, который следует ожидать при работе станка или технологического процесса при установленном допуске и неизвестном уровне настройки. Считается, что точность станка или технологического процесса известна или достаточно точно оценена заранее;
• точечная оценка доли распределения случайной величины в заданном интервале (L, M) и вне его при неизвестной дисперсии. Пример тот же, но точность заранее неизвестна;
• определение верхней и нижней доверительных границ для доли распределения случайной величины в одностороннем интервале и вне его с заданной нижней границей (а — дисперсия известна, б — дисперсия неизвестна). Пример: определение уровня несоответствий для показателя «процент несоответствий» в металлургии. Случай, когда необходима определенная уверенность в том, что уровень несоответствий не превышает установленного предельного процента;
• определение верхней и нижней доверительных границ для доли распределения случайной величины в одностороннем интервале и вне его с заданной верхней границей (а — дисперсия известна, б — дисперсия неизвестна). Пример тот же, граница меняется;
• определение верхней и нижней доверительных границ для доли распределения случайной величины в заданном интервале и вне его (а — дисперсия известна, б — дисперсия неизвестна). Пример: доказательство (с заданной вероятностью) того, что уровень несоответствий по данному показателю качества превышает установленное в нормативной документации предельное значение. Случай предъявления рекламаций на серийную или массовую продукцию по определенному показателю качества.

Приемочный контроль качества по количественному признаку

Предположим, что выполняется поставка партии изделий потребителю. Качество изделий характеризуется некоторым количественным параметром, который может быть измерен в ходе приемочного контроля поставщика или потребителя. Цель контроля — установление факта соответствия или несоответствия партии требованиям, указанным в условиях договора на поставку. Рассмотрим, как эта задача решается в соответствии с ГОСТ Р 50  779.53−98 «Приемочный контроль качества по количественному признаку для нормального закона распределения».

Согласно ГОСТ контролируемым показателем качества партии является уровень несоответствия, выраженный в виде процента несоответствующих единиц продукции. Несоответствующим считается изделие, показатель качества которого выходит за рамки установленных в ТУ ограничений. Процедуры контроля, применяемые поставщиком и потребителем, имеют некоторые отличия.

В качестве исходных данных, необходимых для расчета контроля поставщика, используются следующие:

• нормативный уровень несоответствий в партии NQL (%);
• нормативный риск β₀ потребителя получить партию, в которой уровень несоответствий превышает нормативный. Величина риска назначается в зависимости от степени доверия к поставщику;
• предельные по ТУ значения показателя качества;
• значение стандартного отклонения показателя качества σ;
• объем выборки n.

Исходные данные для расчета плана контроля потребителя отличаются от приведенных только тем, что вместо риска потребителя задается риск поставщика α, то есть риск бракования годной партии. Такой способ задания исходных данных направлен на то, чтобы поставщик учитывал интересы потребителя, а потребитель — поставщика.

Процедура выборочного приемочного контроля состоит в вычислении по результатам измерений n изделий значения выборочного среднего

и сравнении этой величины с установленными приемочными границами. В зависимости от вида ограничений на параметр по ТУ алгоритм контроля сводится к проверке одного из трех неравенств:

Здесь y— результат однократного измерения, a, b — ограничения по ТУ, k — коэффициент, определяемый по таблицам ГОСТ, σ — среднеквадратическое отклонение параметра качества. На рис. 4 показан фрагмент интерфейса процедуры приемочного контроля. План контроля рассчитывается в процедуре автоматически.

Рис. 4. Фрагмент интерфейса процедуры приемочного контроля по ГОСТ Р 50  779.53−98

Корреляционный анализ для парных наблюдений

На практике зачастую бывает важно установить зависимость между парами соответствующих случайных переменных. Например, определить, зависит ли величина выходного параметра изделия от некоторого внешнего фактора. Визуально связь между двумя переменными хорошо отображается с помощью так называемой диаграммы рассеивания. Для ее построения необходимо расположить парные данные, между которыми предполагается исследовать корреляцию, в смежных столбцах (желательно, чтобы количество пар данных было не менее 30), а затем построить точечную диаграмму. Возможны варианты положительной корреляции, когда облако рассеяния на диаграмме имеет вид эллипса с положительным наклоном его главной оси; отрицательной корреляции, когда облако рассеяния на диаграмме имеет вид эллипса с отрицательным наклоном; отсутствия корреляции, когда рассеяние имеет вид круга. Диаграмма рассеяния для парных наблюдений дает качественную оценку статистической связи между переменными. Для оценки силы связи в количественных терминах производится вычисление выборочного коэффициента корреляции r. Коэффициент корреляции принимает значения из диапазона -1 ≤ r ≤ 1. В случае сильной положительной корреляции коэффициент стремится к значению +1, сильной отрицательной корреляции — к значению -1, а при отсутствии корреляции — к значению 0. Предположим, что данные имеют двумерное нормальное распределение с генеральным коэффициентом корреляции, равным ρ. Даже если ρ=0, выборочный коэффициент корреляции r не будет равен нулю. Можно показать, что статистика

имеет t-распределение с (n-2) степенями свободы. Задав уровень значимости α для решения, можно проверить гипотезу H₀ о равенстве нулю генерального коэффициента корреляции против альтернативы H₁ о неравенстве этого коэффициента нулю.

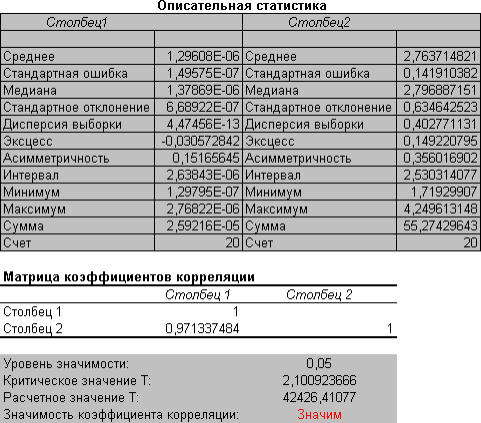
Пример. Методом литья под давлением изготавливается корпус для изделия. Предприятие сталкивается с трудностями из-за дефектных корпусов, имеющих слишком тонкие стенки. Было высказано предположение, что причина дефектности — в вариации давления сжатого воздуха, которое каждый день меняется. Корреляционный анализ данных о толщине стенок и давлении сжатого воздуха позволяет подтвердить или опровергнуть данное предположение. На рис. 5 показана выходная форма, в которой отражены результаты корреляционного анализа для парных наблюдений.

Рис. 5. Выходная форма инструмента корреляционного анализа

Дисперсионный однофакторный анализ

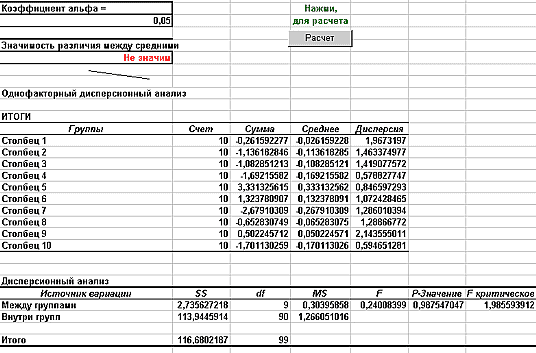
Приведем пример производственной ситуации, поясняющей сущность дисперсионного анализа. Для обеспечения необходимых объемов выпуска при серийном производстве нередко осуществляется одновременное изготовление изделий на нескольких однотипных технологических установках. Чтобы быть уверенным в получении однородной совокупности изделий, необходимо узнать, является ли работа однотипных установок идентичной. Здесь можно было бы применить критерий Стьюдента для попарного сравнения средних арифметических, полученных из совокупностей изделий, изготовленных на соответствующих установках, но предпочтительнее метод разложения дисперсий или дисперсионный анализ. Этот метод основан на том, что при различии в работе технологических установок частные средние, вычисленные по выборкам, отличаются друг от друга более, чем можно было бы ожидать на основе случайных колебаний отдельных значений контролируемого параметра качества. На рис. 6 показана выходная форма с результатами дисперсионного анализа по десяти переменным.

Рис. 6. Результаты дисперсионного анализа

Проектирование организационной структуры контроля

В заключение рассмотрим одно из перспективных направлений разработки. На сегодня при проектировании технологического процесса в системе TechnologiCS считается, что организационная структура контроля задана заранее (под организационной структурой понимается размещение операций контроля, состав контролируемых параметров и точность, с которой они измеряются). Задача проектирования структуры решается преимущественно на эмпирическом уровне, на основе опыта разработчиков. Методической основой в какой-то степени может служить ГОСТ 14.306−73. В известных нам процедурах ИСО эта задача еще не нашла отражения. Но эмпирический подход не гарантирует, что будет найдена оптимальная структура контроля, а значит потери производства, соответствующие разным решениям, могут колебаться в широких пределах. Если же структура контроля задана неверно, это может свести на нет последующие усилия по удержанию процесса в статистически устойчивом состоянии.

Для решения задачи проектирования организационной структуры контроля разработан математический аппарат, с помощью которого находится такое размещение контрольных операций в ТП и такая точность контрольного оборудования, которые гарантируют минимальные суммарные средние потери при производстве изделий ³. Потери складываются из затрат на восстановление пропущенного при контроле брака и затрат на контроль. Для контроля группы из m технологических операций суммарные средние потери рассчитываются по формуле

где 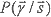- вероятность принятия решения при условии, что истинное состояние объекта контроля ,
 — априорная вероятность состояния объекта контроля,
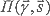- потери принятия решения при состоянии объекта .

Решение задачи требует значительного объема исходной информации. Реальные очертания оно приобретает только сейчас: до появления системы управления производством со встроенными в нее статистическими процедурами получить такую информацию было невозможно.

Скачать статью в формате PDF — 496.2 Кбайт